线段树

作用：对【l，r】区间进行修改操作，询问【l，r】区间的某种性质（最大值，前缀和等等）
操作：
1.build：将一段区间初始化成线段树
2.modify：修改操作，有两种，一种是修改单点（简单），一种是修改区间（要用到懒标记）
3.query：查询某个区间的操作
更新：
1.push up：由子树来更新父结点的信息
2.push down：父结点的修改信息下传到子结点

结构：是一个二叉树，如果【l，r】是根结点的区间，那么他的左子树的区间就是【l，mid】，右子树的区间是【mid+1,r】(mid=l+r/2)

用一个一维数组存，编号：如果一个结点是x，那么他的父节点是x/2-->x>>2;他的左子树是2x-->x<<1;他的右子树是2x+1-->x<<1|1

最坏情况有 4* n个点，所以我们直接开4*n个空间来存

1.创建树：build函数

先把左右端点存入结构体中，如果左右端点一样说明我们走到了根结点直接返回，否则我们算一下这个左右端点的中间值，建他的左右子树

void build(int u,int l,int r){
	tr[u].l =l,tr[u].r =r;
	if(l==r)return ;
	int mid=l+r>>1;
	build(u<<1,l,mid),build(u<<1|1,mid+1,r);
	pushup(u);
}

修改操作：（单点修改）

把x这个点修改成v
当这个结点就是根结点x那么就直接修改；
如果不是，比较x与mid=tl+tr>>1的关系
如果x<=mid,我们就修改左子树，否则修改右子树，
记得每次修改完子树之后我们还要pushup操作一下（子树的内容变化我们要及时根据子结点更新父结点内容）

void modify(int u,int x,int v){
	if(tr[u].l==x&&tr[u].r==x)tr[u].v=v;
	else{
		int mid=tr[u].l+tr[u].r>>1;
		if(x<=mid)modify(u<<1,x,v)
		else modify(x<<1|1,x,v);
		pushup(u);
	}
}

修改操作：（区间修改）

修改区间：懒标记add 给当前结点为根的子树中的每个节点加上add（不包括当前区间自己） 然后对于每次的修改操作，先判断当前子树是不是被要修改的区间完全包含
如果完全包含的话就直接把这个区间加上懒标记更新一下其他参数
如果不完全包含的话说明需要分裂，那么我们就进行pushdown操作
然后当区间与子树的左边有交集（l<=mid）修改左边
当与右边有交集（r>mid）修改右边
每次修改完之后还需要pushup一下

以每个区间的数都加上一个数为例

void modify(int u,int l,int r,int d){
	if(tr[u].l >=l&&tr[u].r <=r){
		tr[u].sum +=(ll)(tr[u].r -tr[u].l +1)*d;
		tr[u].add +=d;
	}else{
		pushdown(u);
		int mid=tr[u].l +tr[u].r >>1;
		if(l<=mid)modify(u<<1,l,r,d);
		if(r>mid)modify(u<<1|1,l,r,d);
		pushup(u);
	}
	
}

pushdown函数：
当从上往下递归的时候，当前的区间不满足我们查询的区间，我们把他的懒标记传到子节点，然后给把他本身的懒标记清空，继续递归到子节点

//以区间每个数都加一个数为例，下传add结点
void pushdown(int u){
	tr[u<<1].add+=tr[u].add;
	tr[u<<1|1].add+=tr[u].add;
	tr[u<<1].sum+=(tr[u<<1].r-tr[u<<1].l+1)*tr[u].add;
	tr[u<<1|1].sum+=(tr[u<<1|1].r-tr[u<<1|1].l+1)*tr[u].add;
	tr[u].add=0;
}

查询操作：query函数

对单点修改的查询：
比如我们要查讯的区间是[l,r],这时递归到的树的结点是u，包含的区间是[tl,tr]
有有两种情况：
（1）当这个结点所包含的区间里完全被包含在要查询的区间，那么直接返回这个结点的相应性质
（2）当有交集的时候：
（如果是区间修改的时候，我们向下分裂查询需要pushdown一下）
1.l<=mid,说明要查询的区间与这个结点的左子树有交集，我们递归左子树
2.r> mid,说明要查询的区间与这个结点的右子树有交集，我们递归右子树
例如：我们要查l，r区间的最大值，v表示最大值

int query(int u,int l,int r){
	if(l<=tree[u].l&&r>=tree[u].r) return tree[u].v;
	int mid=tree[u].l+tree[u].r>>1;
	int v1=-1,v2=-2;
	if(l<=mid)v1=query(u<<1,l,r);
	if(r>mid)v2=query(u<<1|1,l,r);
	int v=max(v1,v2);
	return v;
}

对区间修改的查询：
对于每次查询，先看查询的区间是不是完全覆盖当前子树的区间，如果是的话返回这个子树的参数，如果不是，那我们就要分裂，分裂就需要pushdown，之后在判断与左右子树有无交集分别查询

ll query(int u,int l,int r){
	if(l<=tr[u].l &&r>=tr[u].r ){
		return tr[u].sum ;
	}
	pushdown(u);
	int mid=tr[u].l +tr[u].r >>1;
	ll ans=0;
	if(l<=mid)ans+=query(u<<1,l,r);
	if(r>mid)ans+=query(u<<1|1,l,r);
	return ans;
}

区间乘一个数再加一个数

思路：可以知道先乘后加比较好转换形式，比如原来的柿子是x×a+c
那我们再把这个数×b+c之后的形式就是xab+cb+c
那么我们就可以得到每次修改就是将原来的mul 新的mul，原来的add改为原来的add*新的mul+新的add
然后对于每个操作，加上一个数的话mul=1，乘一个数的话add=0

void even(name &t,ll add,ll mul){
	t.sum =(t.sum *mul+add*(t.r -t.l +1))%p;
	t.add =(t.add *mul+add)%p;
	t.mul =t.mul *mul%p;
}
void pushdown(int u){
	even(tr[u<<1],tr[u].add ,tr[u].mul );
	even(tr[u<<1|1],tr[u].add ,tr[u].mul );
	tr[u].add =0;
	tr[u].mul =1;
}

扫描线

问题：在一个直角坐标系中有很多个矩形，求所有矩形覆盖面积之和

保证所有矩形都在第一象限

解法：模拟一根线在坐标系上扫（从左往右或者从上到下）

这里我们模拟从左往右扫：

假设最后所有矩形的覆盖面积如图：

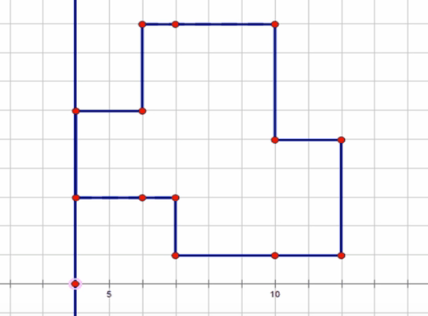
我们可以用一根线来从左往右扫，扫到边变化的位置的时候计算一下面积，例如：

刚开始的线如图：

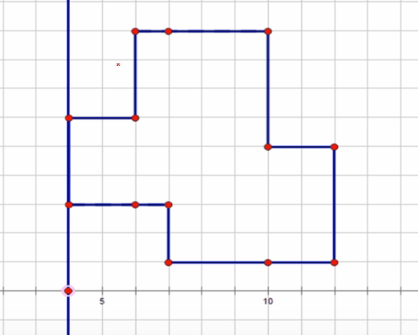
我们走到边变化的位置：

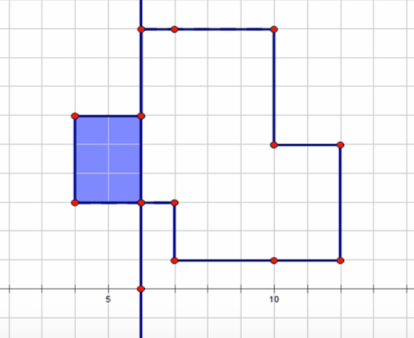
那么经过的面积就是横坐标变化量乘上扫描线的长度：x*len

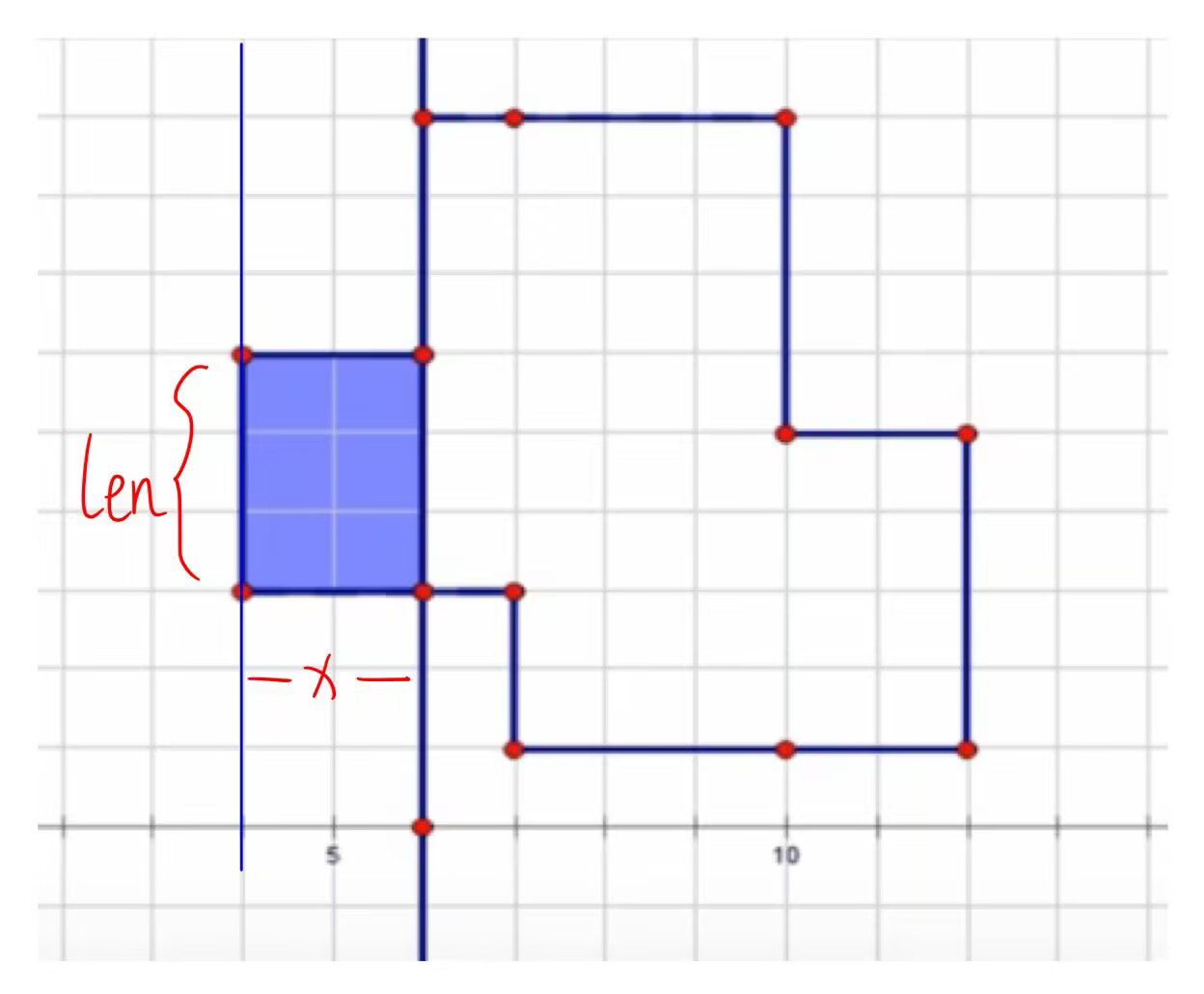
再继续这样扫描，每次扫描都计算一下面积，把所有的面积都加起来就是最终答案

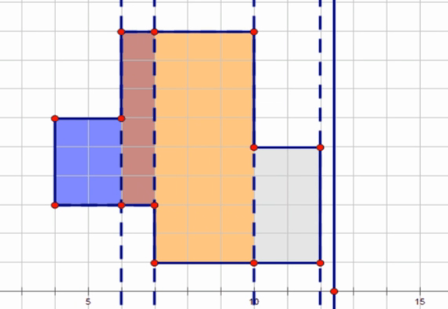
可以发现，扫描线的长度是一直在变化的

可以把扫描线视为一个无限长的与y轴平行的数轴，并赋予每个坐标一个属性cover代表在这个坐标上数轴被矩形覆盖的次数。每次碰到一个矩形的左边后，我们就将这个矩形覆盖的区间的cover++，碰到一个矩形的右边后就让这个矩形覆盖的坐标的cover--，那么当一个区间的cover值大于0的话就说明这个区间还被矩形覆盖，就需要算这个区间的长度

那么对y轴建立一个线段树来维护扫描线，每次碰一个边就对线段树进行一次操作，并且对于较大的坐标范围需要进行离散化操作

由于查询的时候直接查询整个区间的sum值，所以不需要pushdown分裂操作，每次修改子区间之后将子区间pushup更新一下父节点一直更新到根节点的sum就可以了

小细节：y有两个，所以线段树要开到数据的两倍*N

例题：https://www.luogu.com.cn/problem/P8648

#include<bits/stdc++.h>
using namespace std;
int n;
const int N=3e5+10;
typedef long long ll;
struct name{
	int l,r,cover;
	ll sum;
}tr[N*4];
vector<int> y;
struct name1{
	int x,y1,y2,d;
}q[N*4];
bool cmp(name1 a,name1 b){
	return a.x <b.x ;
}

int findy(int xx){
	return lower_bound(y.begin(),y.end(),xx)-y.begin();
}
void build(int u,int l,int r){
	tr[u].l =l,tr[u].r =r;
	tr[u].cover =0;
	tr[u].sum =0;
	if(r-l==1)return ;
	int mid=l+r>>1;
	build(u<<1,l,mid);
	build(u<<1|1,mid,r);
}
void pushup(int u){
	if(tr[u].cover >0) tr[u].sum =y[tr[u].r ]-y[tr[u].l ];
	else tr[u].sum =tr[u<<1].sum +tr[u<<1|1].sum ;
}

void modify(int u,int l,int r,int d){
	if(l==r)return ;
	if(l<=tr[u].l &&r>=tr[u].r ){
		tr[u].cover +=d;
		pushup(u);
	}else{
		int mid=tr[u].l +tr[u].r >>1;
		if(l<mid)modify(u<<1,l,r,d);
		if(r>mid)modify(u<<1|1,l,r,d);
		pushup(u);
	}
}
int main(){
	cin>>n;
	int con=0;
	for(int i=1;i<=n;i++){
		int x1,x2,y1,y2;
		cin>>x1>>y1>>x2>>y2;
		int mix=min(x1,x2);
		int mxx=max(x1,x2);
		int miy=min(y1,y2);
		int mxy=max(y1,y2);
		q[++con]={mix,miy,mxy,1};
		q[++con]={mxx,miy,mxy,-1};
		y.push_back(y1);
		y.push_back(y2);    
	}
	sort(y.begin() ,y.end() );
	y.erase(unique(y.begin() ,y.end() ),y.end() );	 
	sort(q+1,q+1+con,cmp);
	int op=y.size();
	build(1,0,op-1);
	modify(1,findy(q[1].y1) ,findy(q[1].y2) ,q[1].d );
	ll ans=0;
	for(int i=2;i<=con;i++){
		ans+=(q[i].x -q[i-1].x )*tr[1].sum ;
		modify(1,findy(q[i].y1) ,findy(q[i].y2) ,q[i].d );
	}
	cout<<ans;
	return 0;
}