模拟栈，模拟队列

栈

先进先出，如图，栈像一个桶，进入的顺序是1，2，3，从桶里拿出的顺序是3，2，1：

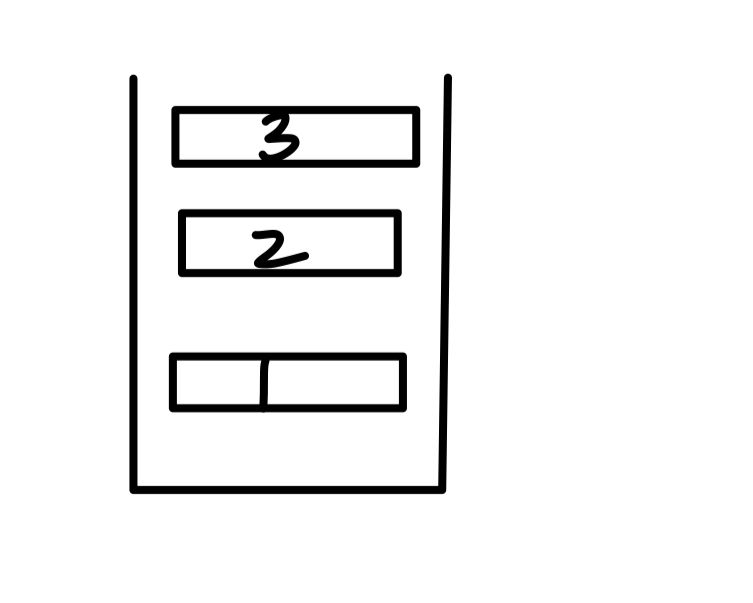
用数组stk[n]模拟栈，tt存的是栈顶元素的下表。

int stk[N];
int tt;
//加入栈
stk[++tt]=x;
//移除栈顶元素
tt--;
//判断栈是否为空
if(tt>0) not empty;
else empty;
//输出栈顶元素
stk[tt];

队列

先进先出，如图，在通道处排队出去，排在前面的先出

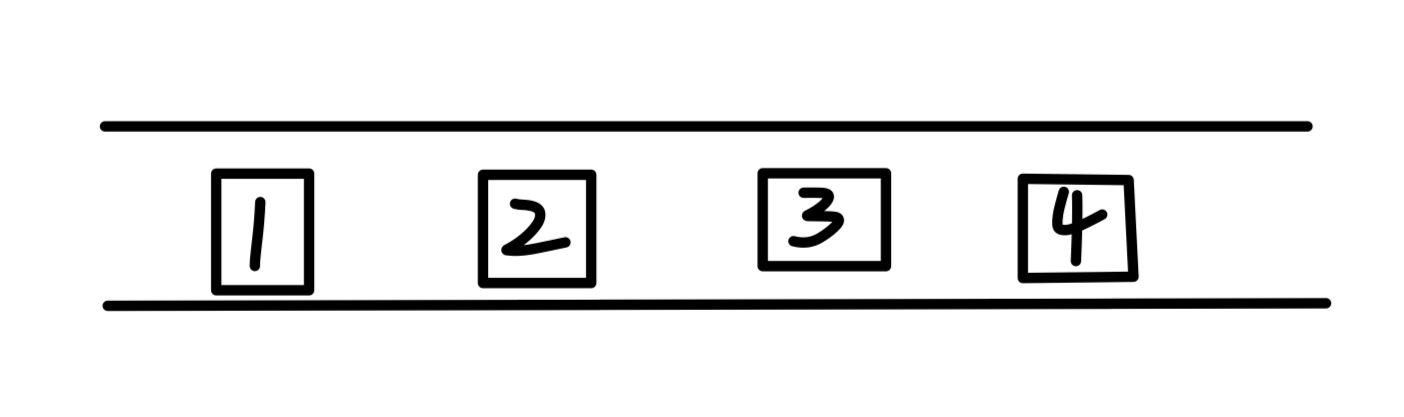
用两个指针hh和tt分别指向队头和队尾，初始化的时候tt在hh前面，当从队尾进的时候q[++tt]=x,在队头出的时候hh--，队列如果不为空，那么tt>=hh。

单调栈

解决问题：给出一个数组，找出每个数的左边第一个小于自己的数，如果没有输出-1

暴力做法是，先枚举每个数，然后从他的前一个数开始向左枚举，直到找到第一个小于这个数的时候停止。

那么我们可以发现，一些数是永远不会被当作答案输出的。

那么我们可以发现，当i< j的时候，如果a[i]> a[j], 那么a[i]永远不会被当做答案输出。因为对于j右边的数x来说，j是离他们最近的，而且a[j]< a[i]，所以如果a[j]< x，那么首选a[j]，如果a[j]>x,那么a[i]>x，也不满足条件。

那么利用这个性质，我们可以模拟一个栈，栈中为前面的数，当遍历到j的时候，我们找到自顶到底第一个小于a[j]的数，并把他上面的数全从栈顶弹出（因为他们不会被当作答案输出），然后再将a[j]加入

#include<iostream>
#include<algorithm>
using namespace std;
int n,m;
const int N=300005;
int stk[N];
int tt;

int main(){
    cin>>n;
    for(int i=1;i<=n;i++){
        int x;
        cin>>x;
        while(tt>0&&stk[tt]>=x){
            tt--;
        }
        if(tt>0)cout<<stk[tt]<<" ";
        else cout<<"-1 ";
        stk[++tt]=x;
    }
    return 0;
}

单调队列

滑动窗口：一个数组里有n个数，有一个长为k的窗口，从数组的最左边移动到数组的最右边，每次向右移动一个位置，求每次移动时窗口内的最大最小值。

那么对于每次移动，就相当于一个长度为k的队列，在队尾加入一个数，然后在队头弹出一个数。然后在队列内找出最大值和最小值。

先找窗口中的最小值：我们可以发现，对于i< j时，a[i]>a[j]的情况，如果a[j]入队答案肯定不会是a[i]，并且a[i]会比a[j]更早出队，那么a[i]将不会被作为答案输出。

如图：当窗口位置如下图的情况时，最小的答案为1

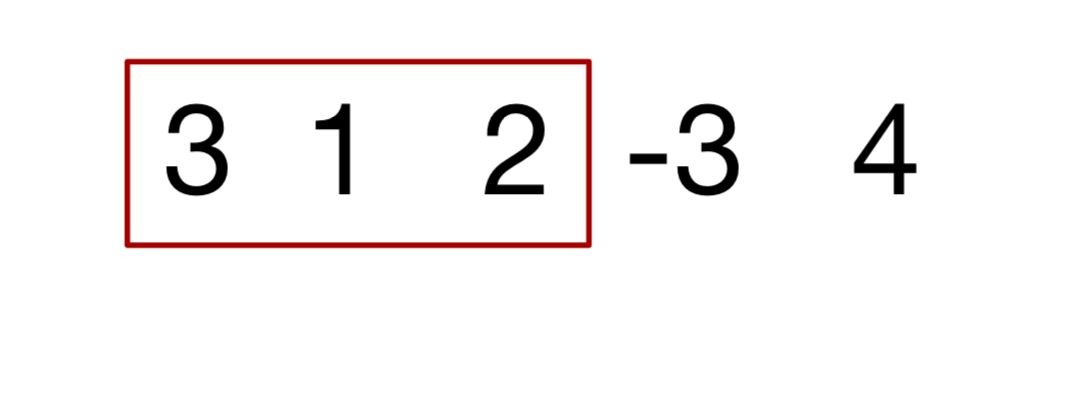
那么窗口向右移动一格，-3进入，为最小的数，无论窗口向后移动多少格，1和2都不会做为最小的数输出

那么我们就可以模拟一个单调队列，每次加入一个数之前，先判断队头是否在窗口中，如果不在需要弹出队头的数。再将队中所有大于他的数弹出，然后再将他放入队尾。那么最小的数就是队头的数。

注意：与单调栈不同的是，需要判断当前队列中的队头的数是否在窗口中，那么我们就需要用队列存数组的下标，判断的时候直接看队头的下标是否在以i为结尾长度为k的窗口中即可。

#include<iostream>
#include<algorithm>
using namespace std;
int n,k;
const int N=1e6+10;
int q[N],a[N];
int tt,hh;
int main(){
    cin>>n>>k;
    for(int i=0;i<n;i++){
        cin>>a[i];
    }
    tt=-1,hh=0;
    for(int i=0;i<n;i++){
        if(q[hh]<i-k+1)hh++;//q[hh]存的是队头的下标，判断队头是否在以i为结尾的长度为k的窗口里，如果不在弹出队头
        while(tt>=hh&&a[q[tt]]>=a[i]){//将大于a[i]的数弹出
            tt--;
        }
        q[++tt]=i;//将a[i]加到队尾，q记录的是下标
        if(i>=k-1)cout<<a[q[hh]]<<" ";
    }
    return 0;
}