树状数组
作用:单点修改区间查询
1.快速求前缀和 O(logn)
2.快速修改某个数 O(logn)
lowbit(x)表示x的最低位1所表示的十进制数
tr[i]表示区间[1,i]的和
1.求前缀和:
int sum(int x){
int res=0;
for(int i=x;i;i-=lowbit(i) )res+=tr[i];
return res;
}
2.在下标为i的位置上加一个数
void add(int x,int c){
for(int i=x;i<=n;i+=lowbit(i))tr[i]+=c;
}
例题
冒泡排序求交换次数
给定n个数,进行冒泡排序,请计算交换次数。
数据范围:n<=5e5,a[i]<=1e9
本质就是记录逆序对的数量。
先进行离散化,算逆序对的数量。
区间修改,单点查询
有一个大小为n的a数组,每次将下标为l~r的数加上一个数,最后再查询每一个数最终的结果
利用差分数组,设b是a的差分数组,对a的操作相当于b[l]+c,b[r+1]-c,b[1]+b[2]+...+b[i]就是变化之后a[i]的值。
区间修改,区间查询
有一个大小为n的数组,m条指令,每条指令有两种:
1.C l r d,表示把a[l]~a[r]都加上d
2.Q l r,表示询问数列中第l~r的和。
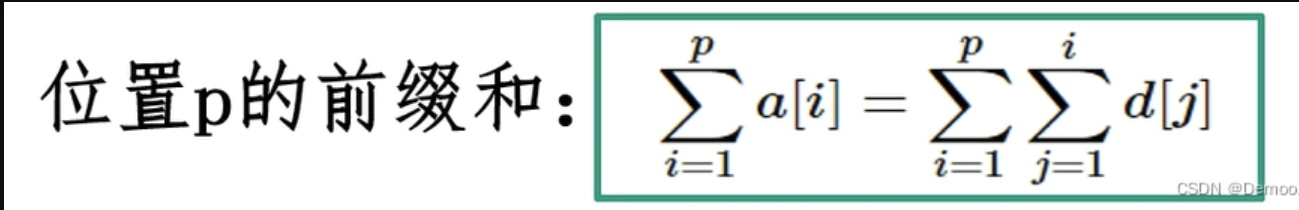

那么要求a[i]的前缀和我们只需要维护两个树状数组:差分数组d和i*d就可以了。
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+10;
int n,m;
int tr1[N*4],tr2[4*N];
int a[N];
int lowbit(int x){
return x&(-x);
}
int sum(int tr[],int x){
int res=0;
for(int i=x;i;i-=lowbit(i)){
res+=tr[i];
}
return res;
}
void add(int tr[],int x,int c){
for(int i=x;i<=n;i+=lowbit(i)){
tr[i]+=c;
}
}
signed main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a[i];
int op=a[i]-a[i-1];
int tmp=op*i;
add(tr1,i,op);
add(tr2,i,tmp);
}
while(m--){
char op;
cin>>op;
if(op=='C'){
int l,r,d;
cin>>l>>r>>d;
add(tr1,l,d);
add(tr2,l,l*d);
if(r+1<=n){
add(tr1,r+1,-d);
add(tr2,r+1,(r+1)*(-d));
}
}else{
int l,r;
cin>>l>>r;
int sumr=(r+1)*sum(tr1,r)-sum(tr2,r);
int suml=(l)*sum(tr1,l-1)-sum(tr2,l-1);
cout<<sumr-suml<<endl;
}
}
return 0;
}
约瑟夫问题
有n个人按顺序围成一圈,编号为1的人从1开始喊,喊到m的人出局,直至没有人,求出局的顺序。
思路:其实就是存在的人从1喊到m,存在且喊到m的人出局
假设下标从1开始,从now开始喊,那么下一个喊到的人应该是now+m-1
但是由于喊出的人要出局,当前人数会有变化,假设当前人数为op,那么我们就得将now映射到1~op序号里
那么我们先将now+m-1减去1,将他映射到0n-1的序号里,再%op将他映射到0op-1的序号里,最后加上1将他映射到1~op的序号里,即下次喊到m的人的序号x是:x=(now+m-1-1)%op+1
上面我们算的是当人都存在的时候,喊到的人的序号,那么随着出局会有人不存在,那么我们就用树状数组来记录每个人存在与否,每个人的位置刚开始都为1表示都存在,当他喊到的时候将他位置上的数-1,并且将记录当前人数的op--。由于x算的是从存在的人里算出的序号,那么我们最终算的人的真实序号id其实是满足sum(id)==x的id,id用二分求出,然后直接输出即可
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=200;
int n,m;
int a[N];
int tr[4*N];
int lowbit(int x){
return x&(-x);
}
int sum(int x){
int res=0;
for(int i=x;i;i-=lowbit(i))res+=tr[i];
return res;
}
void add(int x,int c){
for(int i=x;i<=n;i+=lowbit(i))tr[i]+=c;
}
bool cheek(int x,int s){
if(sum(x)>=s)return true;
else return false;
}
void sove(){
cin>>n>>m;
int now=1;
int op=n;
for(int i=1;i<=n;i++)add(i,1);
while(op){
now=(now+m-1-1)%op+1;
int l=1,r=n;
while(l<r){
int mid=l+r>>1;
if(cheek(mid,now))r=mid;
else l=mid+1;
}
cout<<l<<" ";
add(l,-1);
op--;
}
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(),cout.tie();
int t=1;
// cin>>t;
while(t--){
sove();
}
return 0;
}
二维树状数组
例题:红色的幻想乡
原题链接:https://www.luogu.com.cn/problem/P3801
题意:有一个n*m的矩阵,q个操作,有两种:
1 x y:在(x,y)这个地方向上下左右四个方向放迷雾
2 x1 y1 x2 y2:求以(x1,y1)为左上角,(x2,y2)为右下角的矩形内有多少个格子被雾覆盖
如果一个格子原来有雾气,再放一个雾,两个雾相遇会消散。
思路:用两个树状数组来维护行和列,每次在(x,y)这个地方放的时候,相应的第x行和第y列就会增加一个雾,因为两个雾会消散,所以我们要额外用一个数组记录他放雾之前的状态,如果之前是0的话这一行(或列)就+1,如果是1的话就-1.
那么如果要求以(x1,y1)为左上角,(x2,y2)为右下角的矩形内有多少个格子被雾覆盖的话,设x0为x1x2有几行是1,y0为y1y2有几列是1,那么结果就是x0*(y2-y1+1)+y0*(x2-x1+1)-x0* y0*2(重合的部分消散,等于多算了两遍)
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+20;
#define int long long
int n,m,q;
int tx[N],ty[N];
bool dx[N],dy[N];
int lowbit(int x){
return x&(-x);
}
int sumx(int x){
int ans=0;
for(int i=x;i;i-=lowbit(i)){
ans+=tx[i];
}
return ans;
}
int sumy(int x){
int ans=0;
for(int i=x;i;i-=lowbit(i)){
ans+=ty[i];
}
return ans;
}
void addx(int x,int c){
for(int i=x;i<=n;i+=lowbit(i)){
tx[i]+=c;
}
}
void addy(int x,int c){
for(int i=x;i<=m;i+=lowbit(i)){
ty[i]+=c;
}
}
signed main(){
cin>>n>>m>>q;
while(q--){
int op;
cin>>op;
if(op==1){
int x,y;
cin>>x>>y;
if(!dx[x]){
addx(x,1);
dx[x]=1;
}else{
addx(x,-1);
dx[x]=0;
}
if(!dy[y]){
addy(y,1);
dy[y]=1;
}else{
addy(y,-1);
dy[y]=0;
}
}else{
int x1,y1,x2,y2;
cin>>x1>>y1>>x2>>y2;
int x0=sumx(x2)-sumx(x1-1);
int y0=sumy(y2)-sumy(y1-1);
int ans=x0*(y2-y1+1)+y0*(x2-x1+1)-x0*y0*2;
cout<<ans<<endl;
}
}
return 0;
}
