手写堆

手写堆

以小根堆为例：
操作：
1.插入一个数
2.求集合当中的最小值
3.删除最小值
4.删除任意一个元素
5.修改任意一个元素

结构是一个二叉树，每个点都小于等于左右儿子，那么根节点就是整个树的最小值。 堆的存储：
用一个一维数组来存，一号点是根节点，节点x的左儿子是x<<1,右儿子是x<<1|1.
基本操作：
down(x)：向下调整。假设我们修改一个数，将他改为一个比他大的数x，由于左右子树都得比父节点大，那么我们需要往下调整，将他和他的左右儿子中最小的数交换。如果交换之后x还是比他的左右儿子大，那么再将他与左右儿子中最小的交换。
例如有一个结构为下图的堆：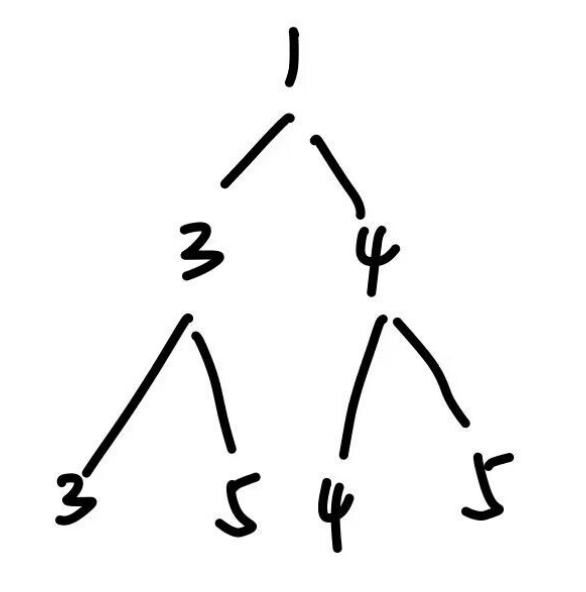

把1改为6的操作：
先将1改为6，因为6比3和4大，那么我们将6和3交换，交换之后6比3和5大，然后我们再将6和3交换。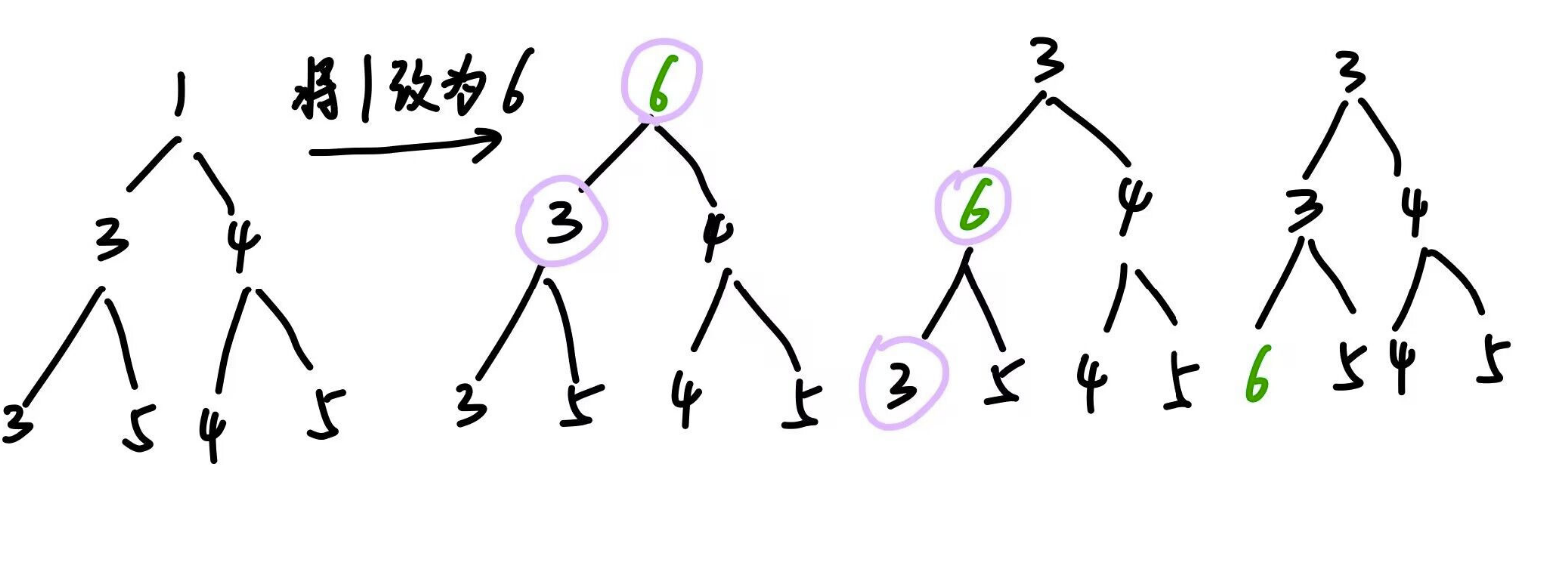

up（x）：往上调整。假设我们修改一个数，将他变为更小的数x，那么我们就需要将他与他的父节点比较，如果x小于他的父节点，那么他就与父节点交换。

down(x)

void down(int x){
    int t=u;//记录最小值的编号
    if((u<<1)<=con&&h[u<<1]<h[t]) t=u;
    if((u<<1|1)<=con&&h[u<<1|1]<h[t])t=u;
    if(t!=u){
        swap(h[u],h[t]);
        down(t);
    }
}

up(x)

void up(int u){
    while(u/2&&h[u/2]>h[u]){
        swap(h[u],h[u/2]);
        u/=2;
    }
}

插入一个数

用con来表示堆的大小，heap数组来储存堆，那么我们就先将他加入到数组的最后一个位置：heap[++con]=x,up(con);

求集合当中的最小值

heap[1]

删除最小值

将最后一个数赋值给heap[1]，大小--，再更新一遍大小。
heap[1]=heap[con],con--; down(1)

删除任意一个数

将最后一个数赋给这个数，大小--，再更新一遍大小。
heap[k]=heap[con],con--;
down(k),up(k);

修改任意一个元素

heap[k]=x,down(k),up(k);

例题:
1.堆排序
原题链接：https://www.acwing.com/problem/content/840/
题意：有一个大小为n的数组，输出数组中前m小的值。

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int n,m;
int h[N],con;
void down(int u){
	int t=u;
	if((u<<1)<=con&&h[u<<1]<h[t]) t=u<<1;
	if((u<<1|1)<=con&&h[u<<1|1]<h[t]) t=u<<1|1;
	if(u!=t){
		swap(h[u],h[t]);
		down(t);
	}
}
int main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++)cin>>h[i];
	con=n;
	for(int i=n/2;i;i--)down(i);
	while(m--){
		cout<<h[1]<<" ";
		h[1]=h[con];
		con--;
		down(1);
	}
	return 0;
}

2.模拟堆
原题链接；https://www.acwing.com/problem/content/841/
题意：
维护一个集合，初始时集合为空，支持如下几种操作：
I x，插入一个数x；
PM，输出当前集合中的最小值；
DM，删除当前集合中的最小值（数据保证此时的最小值唯一）；
D k，删除第k个插入的数；
C k x，修改第k个插入的数，将其变为x；
进行n次操作，对于每个第二个操作，输出当前集合的最小值。

思路：
因为up和down操作都是对一个数所在的位置的编号做的，所以我们在对第k个插入的数执行操作的时候需要知道他所在的位置编号，那么我们就用个额外的数组ph来存第k个插入的数的最终所在的位置编号，还得用一个额外的数组来存每个位置上的数是第几个插入的数。因为我们在进行down和up操作的时候只是把值给交换了，交换值之后还需要把他是第几个插入的数的编号交换一下。

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int n,m;
int h[N],con;
int hp[N],ph[N];
void hswap(int a,int b){
	swap(ph[hp[a]],ph[hp[b]]);
	swap(hp[a],hp[b]);
	swap(h[a],h[b]);
}
void down(int u){
	int t=u;
	if((u<<1)<=con&&h[u<<1]<h[t]) t=u<<1;
	if((u<<1|1)<=con&&h[u<<1|1]<h[t]) t=u<<1|1;
	if(u!=t){
		hswap(u,t);
		down(t);
	}
}
void up(int u){
	while(u/2&&h[u/2]>h[u]){
		hswap(u/2,u);
		u/=2;
	}
}
int main(){
	con=0;
	cin>>n;
	m=0;
	while(n--){
		string op;
		cin>>op;
		if(op=="I"){
			int x;
			cin>>x;
			con++;
			m++;
			h[con]=x;
			ph[m]=con;
			hp[con]=m;
			up(con);
		}else if(op=="PM"){
			cout<<h[1]<<endl;
		}else if(op=="DM"){
			hswap(1,con);
			con--;
			down(1);
		}else if(op=="D"){
			int k;
			cin>>k;
			k=ph[k];
			hswap(k,con);
			con--;
			down(k);
			up(k);
		}else {
			int k,x;
			cin>>k>>x;
			k=ph[k];
			h[k]=x;
			up(k);
			down(k);
		}
	}
	return 0;
}