最长上升子序列模型
基本状态：f[i]表示所有以i结尾的最长上升子序列的长度。
时间复杂度：n*n
状态转移：
for(int j=1;j<i;j++)
if(a[j]<a[i]) f[i]=max(f[i],f[j]+1);
那么如果n比较大，就不能用基础解法，这个时候我们就要用到了贪心优化的解法，时间复杂度nlogn
对于一个数，如果我们能将他放在一个较大的数的后面，那么我们也一定能将他放在一个结尾较小的数的后面。比如：8可以放在3后面，8也可以放在1的后面。那么我们可以用一个数组g来存每个长度下的最长上升子序列结尾的最小值，因为贪心的想同样的长度结尾越小，后面能接的数就越多。那么这个序列的值肯定是单调递增的，因为我们存的是每个递增序列结尾的最小值，后一个长度的结尾肯定大于前一个长度的结尾。
那么如果我们想求以a[i]结尾的最长上升子序列的长度，我们可以二分的求这个序列里小于a[i]的最大值所在的长度的结尾g[x]，那么g[x+1]肯定>=a[i],更新一下g[x+1]=a[i]。
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int g[N];
int n;
int a[N];
int main(){
cin>>n;
for(int i=1;i<=n;i++)cin>>a[i];
int len=0;
g[0]=-2e9;
for(int i=1;i<=n;i++){
int l=0,r=len;
while(l<r){
int mid=l+r+1>>1;
if(g[mid]<a[i]) l=mid;
else r=mid-1;
}
g[r+1]=a[i];
len=max(len,r+1);
}
cout<<len<<endl;
return 0;
}
变形
例题：友好城市
原题链接：https://www.acwing.com/problem/content/1014/
题意：
南北两岸各有n个城市，每个城市都有唯一一个与之相连的城市的道路。有n个关系，分别表示南岸位置在x的城市和北岸位置在y城市之间有条道路，求最多的不交叉的道路。
思路：
可以发现：如果想让两个路不交叉的话，在南岸位置靠前的岛连接的对应的北岸的岛的位置肯定小于南岸位置靠后的岛连接的对应的北岸的岛的位置，那么我们将南岸的岛位置从小到大排序。将次序赋值给每条路，如图：
绿色的是北岸的城市按南岸位置大小顺序排序得出的序号，红色是我们选出的一个合法的方案
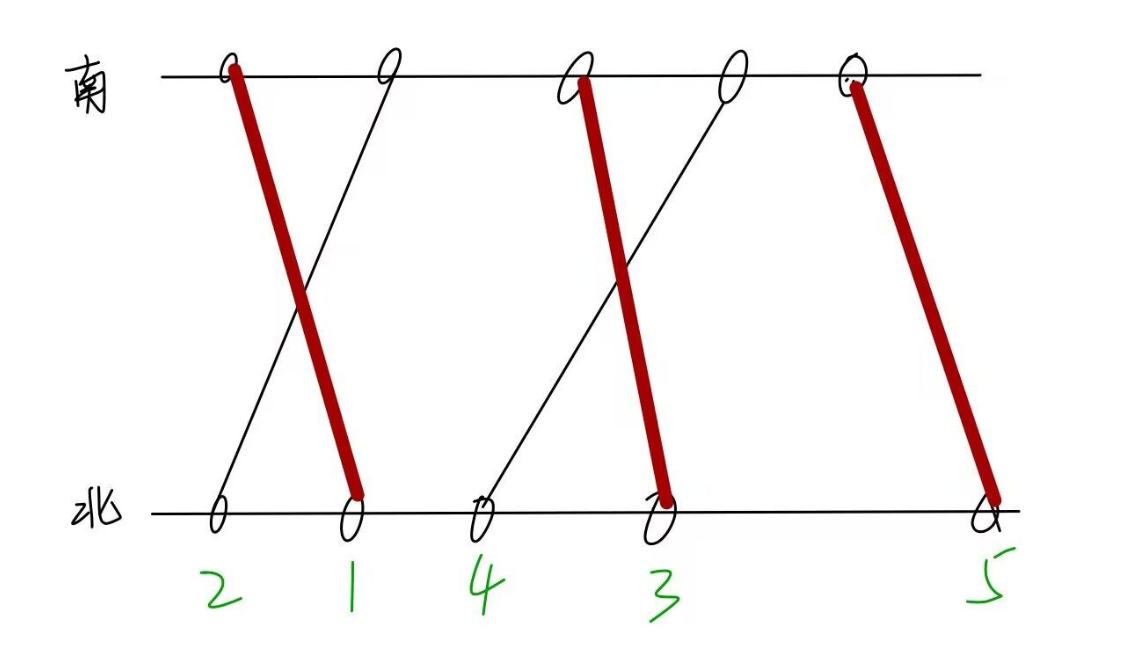然后我们按北岸的位置从小到大选合法方案的时候，需要选序号上升的道路才合法。 那么我们可以发现，合法的方案就是北岸的城市位置从左到右序号的最长上升子序列 #include<bits/stdc++.h>
using namespace std;
const int N=5005;
int f[N];
int n;
struct name{
int x,y,id;
}q[N];
bool cmp1(name a,name b){
return a.x <b.x ;
}
bool cmp2(name a,name b){
return a.y <b.y ;
}
void sove(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>q[i].x>>q[i].y ;
}
sort(q+1,1+q+n,cmp1);
for(int i=1;i<=n;i++) q[i].id =i;
sort(q+1,q+1+n,cmp2);
for(int i=1;i<=n;i++){
f[i]=1;
for(int j=1;j<i;j++){
if(q[j].id <q[i].id )f[i]=max(f[i],f[j]+1);
}
}
int ans=0;
for(int i=1;i<=n;i++){
ans=max(ans,f[i]);
}
cout<<ans<<endl;
}
int main(){
int t=1;
//cin>>t;
while(t--){
sove();
}
return 0;
}
导弹拦截系统
拦截导弹
一个数组最少用多少个非上升的子序列覆盖这个数组中所有数的个数，等于这个数组的最长上升子序列。
原题链接：https://www.acwing.com/problem/content/1012/
题意：
一个导弹拦截系统可以发射许多个拦截导弹，第一个拦截导弹可以发射任意高度，但是以后发射的每一个拦截导弹都不能高于前一个拦截导弹发射的高度，问一个导弹最多能拦截多少导弹，要拦截n个导弹最少需要多少个导弹拦截系统。
思路：
第一问就是求最长不上升子序列。
对于每个导弹，我们有两个选择：
1.放进已有的系统里
2.开一个新的系统放进去
那么贪心的来看：
情况1：如果现有的子序列的结尾都小于这个数，那么我们就新建一个序列把他插进去。
情况2：如果现有的子序列中有结尾大于这个数的序列，就把他放到结尾大于这个数的最小的结尾的子序列中。因为较大的结尾也可以容纳比这个数大的数，后面可能有比这个数更大的数，可以放在较大的结尾后面儿不能放在较小的结尾后面。
实现：用一个g数组来存当前所有开好的子序列的结尾的数，按照贪心的思想放好的子序列的结尾组成一个单调的序列，每一次插入一个数的时候在子序列中找大于等于这个数的最小的一个数所在的序列，将这个数替换；如果找不到，就新开一个子序列来存这个数。那么思想和优化之后的找最长上升子序列的思想差不多，所以侧面证明了求一个数组最少用多少个非上升的子序列覆盖这个数组中所有数的个数等于求最长上升子序列。
最长公共子序列
原题链接：https://www.acwing.com/problem/content/899/
题意：
给定两个长度分别为N和M的字符串A和B，求既是A的子序列又是B的子序列的字符串长度最长是多少。 思路：
f[i][j]表示A的前1i个字符和B的1j个字符中，最长的公共子序列的长度。
以A字符串和B字符串的结尾字符i和j来划分：
公共子序列可以不包含i和j：f[i][j]=f[i-1][j-1]
也可以只包含i：f[i][j]=f[i][j-1]
也可以只包含j：f[i][j]=f[i-1][j]
同时包含ij的话，因为a[i]是a的最后一个元素，b[j]是b的最后一个元素，那么需要满足a[i]==b[j]：if(a[i]==b[j]) f[i][j]=f[i-1][j-1]+1
以上状态取最大值即可。
#include<bits/stdc++.h>
using namespace std;
const int N=1500;
int f[N][N];
int n,m;
int main(){
cin>>n>>m;
string a,b;
cin>>a;
cin>>b;
a=" "+a;
b=" "+b;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
f[i][j]=max(f[i][j],f[i-1][j]);
f[i][j]=max(f[i][j],f[i-1][j-1]);
f[i][j]=max(f[i][j],f[i][j-1]);
if(a[i]==b[j]) f[i][j]=max(f[i][j],f[i-1][j-1]+1);
}
}
cout<<f[n][m]<<endl;
return 0;
}
最长公共上升子序列
原题链接：https://www.acwing.com/problem/content/274/
题意：
有两个数组a，b，求这两个字符串的最长上升子序列。
思路：
求公共子序列设的状态是a的前i个数和b的前j个数组成的最长公共序列的长度。
求上升子序列设的状态是以a[i]结尾的最长上升子序列的长度。
因为a和b是等价的，那么我们用a来解决公共子序列的问题，用b来解决上升子序列的问题。
我们两个问题结合一下得出要设的状态：
f[i][j]表示a的前i个数和b的前j个数构成，且以b[j]结尾的公共上升子序列的最大长度。
按结尾划分就分为包含a[i]和不包含a[i]两种情况。
不包含a[i]的情况就是f[i-1][j]
包含a[i]：前提是a[i]==b[j]。
首先如果只含有a[i]==b[j]这一个子序列的话，长度是1，那么我们先把f[i][j]和1取最大值。
然后枚举倒数第二个结尾的数b[k]，当b[k]< b[j]的时候，说明倒数第二个数可以是b[k]，那么我们就将f[i][k]+1和f[i][j]取最大值。
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
f[i][j]=f[i-1][j];
if(a[i]==b[j]){
f[i][j]=max(f[i][j],1);//当只有一个元素的时候个数是1
for(int k=1;k<j;k++){
if(b[k]<b[j]) f[i][j]=max(f[i][j],f[i-1][k]+1);
}
}
}
}
但是时间复杂度是 会超时，那么我们就需要去优化一下循环。
因为a[i]==b[j]，那么我们将最后一重循环里的if(b[k]<b[j])改为if(b[k]<a[i])，那么最后一个判断就和j没有关系和有关系了，并且表示的意思是在[1~j-1]中找到满足b[k]< a[i]的最大的f[i][k]的值。
那么我们可以边转换边找这个最大值，在j循环之前用一个数maxv来储存第i层循环目前算到的满足条件的最大f值，初始化为0.
那么我们在循环j的时候，如果a[i]==b[j]，那么最后一重循环就可以换成f[i][j]=max(f[i][j],maxv+1),更新完f[i][j]之后，如果b[j]< a[i]，那么说明满足更新maxv的条件，我们更新maxv=max(maxv,f[i][j])。因为我们需要的maxv是[1,j-1]的，所以是在更新完f[i][j]之后再更新maxv。
#include<bits/stdc++.h>
using namespace std;
int n;
const int N=3005;
int f[N][N];
int a[N];
int b[N];
int main(){
cin>>n;
for(int i=1;i<=n;i++)cin>>a[i];
for(int i=1;i<=n;i++)cin>>b[i];
for(int i=1;i<=n;i++){
int maxv=0;
for(int j=1;j<=n;j++){
f[i][j]=f[i-1][j];
if(a[i]==b[j]){
f[i][j]=max(f[i][j],1);
f[i][j]=max(f[i][j],maxv+1);
}
if(b[j]<a[i]) maxv=max(maxv,f[i][j]);
}
}
int ans=0;
for(int i=1;i<=n;i++)ans=max(f[n][i],ans);
cout<<ans<<endl;
return 0;
}