状态压缩dp
定义
状态压缩dp是将比较复杂的状态映射成数字后进行dp
例如:布尔数组用二进制表示(st[i]表示第i位做了还是没做,st数组就可以变成一个二进制数)
更复杂的状态可以用map等结构来重标号成数字后进行转移
滚动数组优化:在转移第i维的时候我们只用到了第i-1维,那么我们就可以用两维相互转化。优化方式:1.将i&1 2.每次用i-1&1维转化完i&1维的时候,要将第i-1&1维清空
类型一:在一个n* m的网格上,用一个图形填网格,有一些限制,求方案数/放的图形的最大最小值
蒙德里安的梦想
题目链接:https://www.acwing.com/problem/content/293/
题意:
有一个NM的矩形,用12的方格将他填满,请问有多少种方法
思路:
如果全部横向的1*2的方格都将当前的矩形放完了,那么剩下的格子都只能放纵向的,所以只需要求只放横向的矩形有多少种方法数就可以了。
横向放从左到右考虑列横着放小方格,因为小方格横跨两列,那么我们考虑到当前列的时候,就需要知道哪些行已经被前一列放的格子占了,如果占了就不能再放横向的小方格了。那么我们就用1来表示放着横向的1* 2的小方格的后面的格子,那么用n位二进制数来记录每当前列每行是否被横向的1*2的小方格的后面的格子占过。
用f[i][j]来表示到第i列时,第i列的行状态为j的方案数
那么需要得到第i列的状态j,那么我们就需要枚举第i-1列的状态k。把所有的满足和j不冲突的状态k的方案加起来,就是状态为j的方案数。
k能转移到j的条件是:
1.两列放的小格子不重叠,如果占的一样就会有下面的情况,不符合题意:
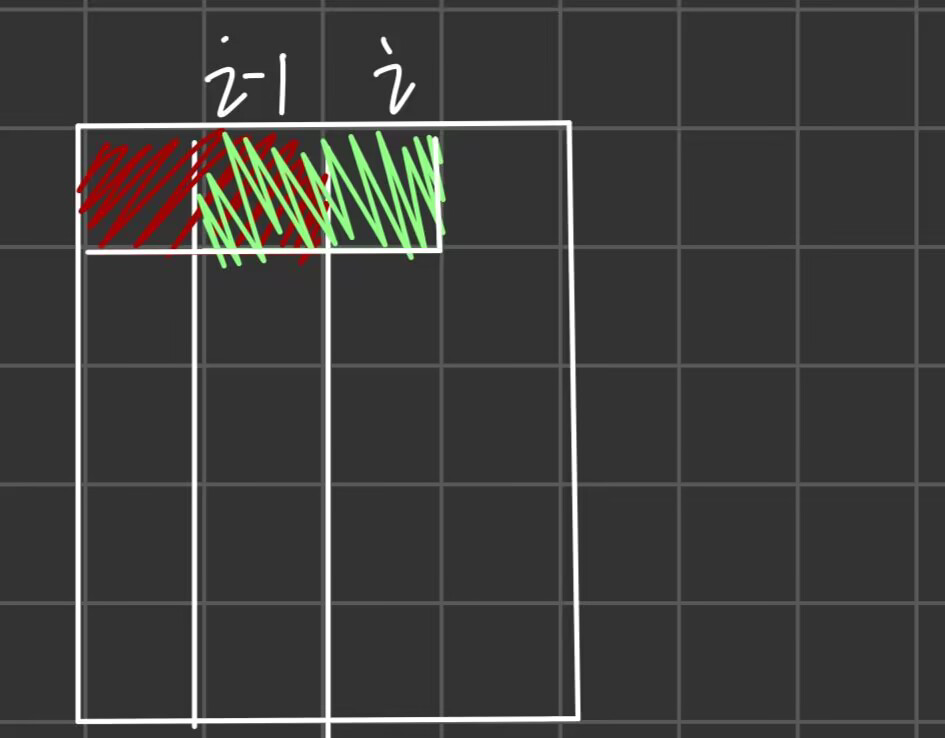
那么就要求k和j的每位不能同时为1,用位运算k&j==0来表示k状态和j状态没有同一行都为1的情况
2.第i-1列的状态k每个1之间相隔的0必须是偶数。
因为我们已经把第i-1列的横向的方格给放完了,剩下的空位都需要用纵向的方格来放,那么我们就必须满足相邻的空出的行是2的倍数。第i列放有横向的12的小方格的后面的格子,那么横向的12的小方格的前面的格子会在第i-1列:
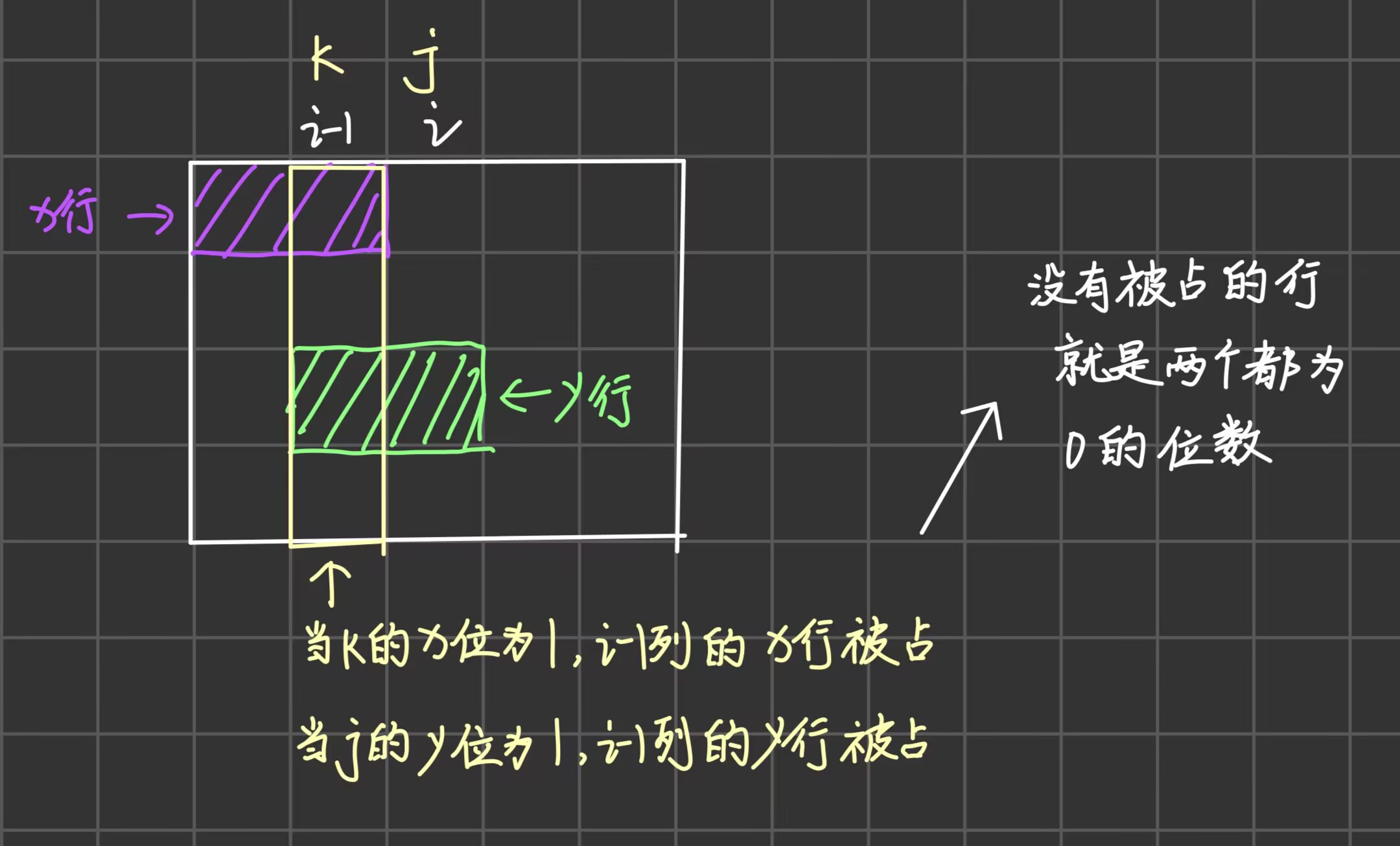
那么i-1列的空格就可以用k|j来算出。
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=12,M=1<<N;
int f[N][M];
int n,m;
bool st[M];
signed main(){
while(cin>>n>>m,n!=0&&m!=0){
for(int i=0;i<(1<<n);i++){
st[i]=true;
int con=0;
for(int j=0;j<n;j++){
if((i>>j)&1){
if(con%2)st[i]=false;
con=0;
}else con++;
}
if(con%2)st[i]=false;
}
for(int i=0;i<=m;i++){
for(int j=0;j<(1<<n);j++){
f[i][j]=0;
}
}
f[0][0]=1;
for(int i=1;i<=m;i++){
for(int j=0;j<(1<<n);j++){
for(int k=0;k<(1<<n);k++){
if((j&k)==0&&st[j|k])f[i][j]+=f[i-1][k];
}
}
}
cout<<f[m][0]<<endl;
}
return 0;
}
炮兵阵地
原题链接:https://www.acwing.com/problem/content/294/
题意:
在n*m的地图上,有p和h两种字符,p可以放炮,h不能放炮,如果在p点放炮,炮的射程是向上,下,左,右的方向各两格,如图:
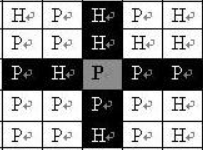
求在任何一个炮都攻击不到其他炮的情况下,整块区域最多能摆放多少炮
思路:
因为列数m比较少,所以我们就将每行的状态压缩
f[i][a][b]表示在前i行被放过的情况下,第i行的状态是a,第i-1的状态是b的放置的炮的最大数量,,cnt[i]是状态为i时炮的个数,目标状态f[n+2][0][0]
假设i-2行的状态是c,那么转移方程就是:
f[i][a][b]=max(f[i][a][b],f[i-1][b][c]+cnt[a])
但是空间会超,我们根据状态转移公式发现f[i]状态只和f[i-1]状态有关,所以进行滚动数组的优化
那么我们只需要预处理出每个合法的状态,然后在枚举合法状态a,b,c的时候判断能不能放,如果能就转移就可以了
状态符合的条件:
1.炮不能相互打到,那么每行的本身状态i的每个1之间的间隔不能少于2,相邻两行的同一列列不能同时出现炮,相隔一行的同一列也没出现炮
2.有h的格子不能放炮
#include<bits/stdc++.h>
#include<vector>
#define int long long
using namespace std;
const int N=11,M=1<<N;
int g[110];
int n,m;
vector<int> stat;
vector<int> h[M];
int cnt[M];
int f[3][M][M];
//检查1的后两格是否有1
bool cheek(int x){
for(int i=0;i<m;i++){
if((x>>i)&1){
if(i+1<m){
int op=x>>(i+1)&1;
if(op)return false;
}
if(i+2<m){
int op=x>>(i+2)&1;
if(op)return false;
}
}
}
return true;
}
//算出每个状态放的炮的个数
int sum(int x){
int ans=0;
for(int i=0;i<m;i++){
if((x>>i)&1)ans++;
}
return ans;
}
signed main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
int ans=0;//将每一行的状态压缩
for(int j=0;j<m;j++){
char x;
cin>>x;
if(x=='H'){
int op=1<<j;
ans+=op;
}
}
g[i]=ans;
}
//预处理出每个状态的炮的个数和合法状态
for(int i=0;i<(1<<m);i++){
cnt[i]=sum(i);
if(cheek(i)){
stat.push_back(i);
}
}
//预处理出相邻的两行的合法状态
for(int i=0;i<stat.size();i++){
for(int j=0;j<stat.size();j++){
int a=stat[i];
int b=stat[j];
if((a&b)==0){
h[a].push_back(b);
}
}
}
for(int i=1;i<=n+2;i++){//枚举每行
for(int j=0;j<stat.size();j++){
int a=stat[j];//枚举第i行的状态a
if((g[i]&a)==0){//如果符合原图条件的放置
for(int k=0;k<h[a].size();k++){
int b=h[a][k];//枚举i-1行状态b
if((g[i-1]&b)==0){//如果符合原图条件的放置
for(int l=0;l<h[b].size();l++){
int c=h[b][l];//枚举i-2行的状态c
if((a&c)==0){//如果a和c没有相同的一列放炮,状态转移
f[i&1][a][b]=max(f[i&1][a][b],f[(i-1)&1][b][c]+cnt[a]);
}
}
}
}
}
}
}
cout<<f[(n+2)&1][0][0];
return 0;
}
类型二:每个点不重不漏走一次,求最短路
最短哈曼顿路径
原题链接: https://www.acwing.com/problem/content/93/
题意:
有n个点,编号0~n-1,求0到n-1的最短哈曼顿路径
哈曼顿路径:每个点不重不漏的走一次
思路:
每个点都走一遍,那么所有的路径的方法数就是n!
用状压dp优化,f[i][j]表示从0走到点j,所有点的状态是i的路径的最小值
状态转移:枚举倒数第二个到达的点k,那么到达点k的所有点的状态就是i-(1<< j),从0到j所有点状态是i的最短路径就是:
f[i][j]=min(f[i][j],f[i-(1<<j)][k]+d[k][j]);
符合状态的条件是:i的第j位为1,i去掉j之后的第k位为1
初始化:求最小值,f初始化为极大值。最初的状态是从0开始走到0,所以f[1][0]=0
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=22,M=1<<N;
int n;
int g[N][N];
int f[M][N];
signed main(){
cin>>n;
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
cin>>g[i][j];
}
}
for(int i=0;i<(1<<n);i++){
for(int j=0;j<n;j++){
f[i][j]=1e16;
}
}
f[1][0]=0;
for(int i=0;i<(1<<n);i++){
for(int j=0;j<n;j++){
if(i>>j&1){
for(int k=0;k<n;k++){
int op=i-(1<<j);
if((op>>k)&1){
f[i][j]=min(f[i][j],f[i-(1<<j)][k]+g[k][j]);
}
}
}
}
}
cout<<f[(1<<n)-1][n-1];
return 0;
}
类型三:要求必须有某些状态,求方案数
I Pa?sWorD
原题链接:
https://pintia.cn/problem-sets/1703372159713652736/exam/problems/1703372337216602120?type=7&page=0
题意:
有一个长度为n的字符串,含有大写字母,小写字母,数字和'?'
大写字母和数字表示本身
小写字母可以为本身,也可以变为对应的大写字母
'?'是不确定的字符,可以变成大写字母,小写字母或者数字
如果这个字符串要成为密码的话,就需要含有至少一个大写字母,至少一个小写字母和至少一个数字,并且相邻的两个字符不能相同。求所有的可能的密码个数,结果对998244353取模。
思路:
分析状态:前i个是一维状态;因为要判断相邻的两个字符是否相等,那么我们再用一维状态061来记录是哪个字符;需要看是否有数字,大写字母和小写字母,那么我们再用一维07分别记录状态:二进制第0位为1表示有数字,二进制第1位为1表示有大写,二进制第2位为1表示有小写
那么就用f[i][a][s1]来记录前i位已经确定,第i位字母是a,状态为s1的方案数
那么我们分别需要枚举s[i]可以变成的字母a,当前的状态s1和s[i-1]可以变成的字母b,当前的状态s2.满足当a!=b且s1中有a类型和b类型的字符且s2中有b类型的字符的时候,转移方程为:
f[i][a][s1]=f[i-1][b][s2]
但是这个时候我们的时间复杂度是O(n626277),会超时,所以我们考虑进一步优化
每次到i的时候,我们先算出前面i-1个满足状态为s2的所有方案数,用sum[s2]数组记录
那么我们再枚举s[i]能转化的字母a和状态s1,当状态满足题意时,转化过来的s2只有两种情况:含a类型和不含a类型,那么我们就将s1加上这两种情况:
f[i][a][s1]+=sum[s1];
f[i][a][s1]+=sum[s1-type(a)]
还有一个条件是a!=b,那么我们直接将所有情况减去第i-1位是a的方案数就可以了:
f[i][a][s1]-f[i-1][a][s1]
最后将时间优化为O(n6210),可以通过。
按上面的方法的话,最终数组是f[1e5][70][10],会空间超限。那么我们用滚动数组优化,将i优化为i&1,并且在每次更新完i&1维之后清除掉i-1&1维的数据
#include <bits/stdc++.h>
using namespace std;
#define int long long
int n;
string s;
int f[3][70][10];
const int mod=998244353;
int type(char x){
if(x>='0'&&x<='9')return 0;
if(x>='A'&&x<='Z')return 1;
return 2;
}
int ha(char x){
int op=0;
if(x>='0'&&x<='9'){
op=x-'0';
}
else if(x>='A'&&x<='Z'){
op=x-'A'+10;
}
else {
op=x-'a'+36;
}
return op;
}
vector<char> canbe(char x){
vector<char> ans;
if(x=='?'){
for(int i=0;i<26;i++){
char op;
op=i+'A';
ans.push_back(op);
op=i+'a';
ans.push_back(op);
if(i<10){
op=i+'0';
ans.push_back(op);
}
}
}else{
ans.push_back(x);
if(islower(x)){
ans.push_back(toupper(x));
}
}
return ans;
}
signed main(){
cin>>n>>s;
for(char x:canbe(s[0])){
f[0][ha(x)][1<<type(x)]=1;
}
for(int i=1;i<n;i++){
int sum[8]={0};
for(char x:canbe(s[i-1])){
for(int s2=0;s2<8;s2++){
int oo=s2>>type(x);
if(oo&1) sum[s2]+=f[i-1&1][ha(x)][s2];
}
}
for(char a:canbe(s[i])){
for(int s1=0;s1<8;s1++){
if((s1>>type(a))&1){
int s2=s1;
f[i&1][ha(a)][s1]=(f[i&1][ha(a)][s1]+sum[s2])%mod;
s2=s1-(1<<type(a));
f[i&1][ha(a)][s1]=(f[i&1][ha(a)][s1]+sum[s2])%mod;
f[i&1][ha(a)][s1]=(f[i&1][ha(a)][s1]-f[i-1&1][ha(a)][s1]+mod)%mod;
}
}
}
for(int j=0;j<=67;j++){
for(int k=0;k<8;k++){
f[i-1&1][j][k]=0;
}
}
}
int ans=0;
for(char x:canbe(s[n-1])){
ans=(ans+f[(n-1)&1][ha(x)][7])%mod;
}
cout<<ans;
return 0;
}
