排列数学
CF1422C Bargain
题目描述
Sometimes it is not easy to come to an agreement in a bargain. Right now Sasha and Vova can't come to an agreement: Sasha names a price as high as possible, then Vova wants to remove as many digits from the price as possible. In more details, Sasha names some integer price nn , Vova removes a non-empty substring of (consecutive) digits from the price, the remaining digits close the gap, and the resulting integer is the price.
For example, is Sasha names 12131211213121 , Vova can remove the substring 13121312 , and the result is 121121 .
It is allowed for result to contain leading zeros. If Vova removes all digits, the price is considered to be 00 .
Sasha wants to come up with some constraints so that Vova can't just remove all digits, but he needs some arguments supporting the constraints. To start with, he wants to compute the sum of all possible resulting prices after Vova's move.
Help Sasha to compute this sum. Since the answer can be very large, print it modulo 10^9 + 7109+7 .
输入格式
The first and only line contains a single integer nn ( 1 \le n < 10^{10^5}1≤n<10105 ).
输出格式
In the only line print the required sum modulo 10^9 + 7109+7 .
题意:
给一串数字,数字的长度是1e5
我们可以删除他任意连续长度的子串,剩下的数字组成新一个数。
求删除子串之后的所有情况的数的总和。
思路:我们看每一位对总数的贡献。比如例子:1213121
我们先将他逆转(以便能更好的计算每一位做的贡献)
我们以3举例:
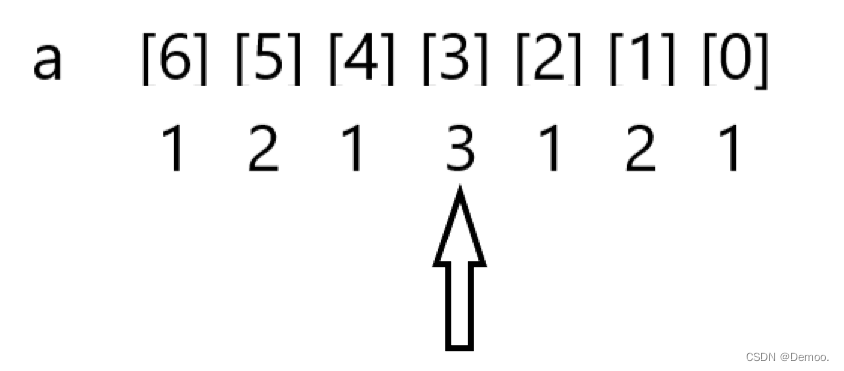
如果3要是对整个数有贡献,那么有两种情况:
1.删除的子串要么在3的前面 2.删除的子串在3的后面。
对于情况1:

红色代表删除的部分。黑色代表留下的部分。
那么3对总数的贡献都没变,就是3*pow(10,i)
那么这种情况有3+2+1=6种,就是看前面有几位数然后从1加到那个数:1+2+...+len-i-1
所以对情况1来说我们总结的a[i]对于总数的贡献就是:
a[i]*pow(10,i)*(len-i-1)*(len-i)/2.
对于情况2:

那么3的位数在变化
当去掉3位的情况有1种,对整体的贡献是pow(10,0):1*pow(10,0)
去掉2位的情况有2种,对整体的贡献是pow(10,1):2*pow(10,1)
去掉1位的情况有3种,对整体的贡献是pow(10,2):3*pow(10,2)
而且对3右面的1来说:
去掉2位的情况有1种,对整体的贡献是pow(10,0):1*pow(10,0)
去掉1位的情况有2种,对整体的贡献是pow(10,1):2*pow(10,1)
那么我们就可以递推着来算贡献的位数
设i-1位对总数的贡献是tmp[i-1],那么第i位对总数的贡献就是:
tmp[i]=tmp[i-1]+i*pow(10,i-1)
然后拿这个位数乘上a[i]就是右边所有数对总数的贡献:a[i]*tmp
还有要注意的就是题目给的mod是1e9+7,那么这个数的长度是1e5的话pow(10,i)到最后肯定会超出范围,那么我们就先预处理一下数组f[i]来记录10^i%mod的数到时候直接用就行。
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
typedef long long ll;
string s;
const int N=1e5+5;
ll f[N];
const ll mod=1e9+7;
int main(){
cin>>s;
f[0]=1;
for(int i=1;i<N;i++){
f[i]=f[i-1]*10%mod;
}
reverse(s.begin(),s.end());
ll ans=0;
ll len=s.size();
ll tmp=0;
for(int i=0;i<len;i++){
ll num1=(len-i-1)*(len-i)/2%mod*f[i]*(s[i]-'0')%mod;
ll num2=(s[i]-'0')*tmp%mod;
tmp=((i+1)*f[i]%mod+tmp)%mod;
ans+=(num1+num2)%mod;
ans%=mod;
}
cout<<ans;
return 0;
}
P3166 [CQOI2014]数三角形
题目描述
给定一个 N\times MN×M 的网格,请计算三点都在格点上的三角形共有多少个。注意三角形的三点不能共线。
输入格式
输入一行,包含两个空格分隔的正整数 MM 和 NN 。
输出格式
输出一个正整数,为所求三角形数量。
输入输出样例
输入 #1复制
2 2
输出 #1复制
76
说明/提示
数据规模与约定
对于全部的测试点,保证 1\le N,M\le10001≤N,M≤1000。
思路:方法就是先枚举出所有点能组成的三角形的数量,然后再减去在一条线上的三个点构成的三角形的数量。
公式:
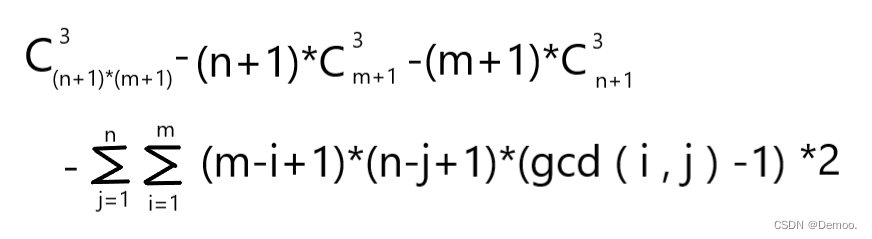
所有点的总数:(n+1)*(m+1)
所有点里挑三个点就是第一个柿子。
然后我们再减去水平边和竖直边里的点构成的三角形的情况,就是第二个和第三个柿子。
最后一个柿子是在一个斜边上的三角形的数量,我们先列举这个斜边是从(0.0)到i,j
i,j就从1~m,1~n。
然后我们就找对于每对的i,j除了两个端点(0,0)和(i,j)中间有几个点在格点上。
以j=6,i=9为例:
(0.0)到(6,9)的点除了两个端点还有gcd(j,i)-1个。
我们把(6.9)看做一个向量,那么我们就是找和这个斜率一样的整数向量
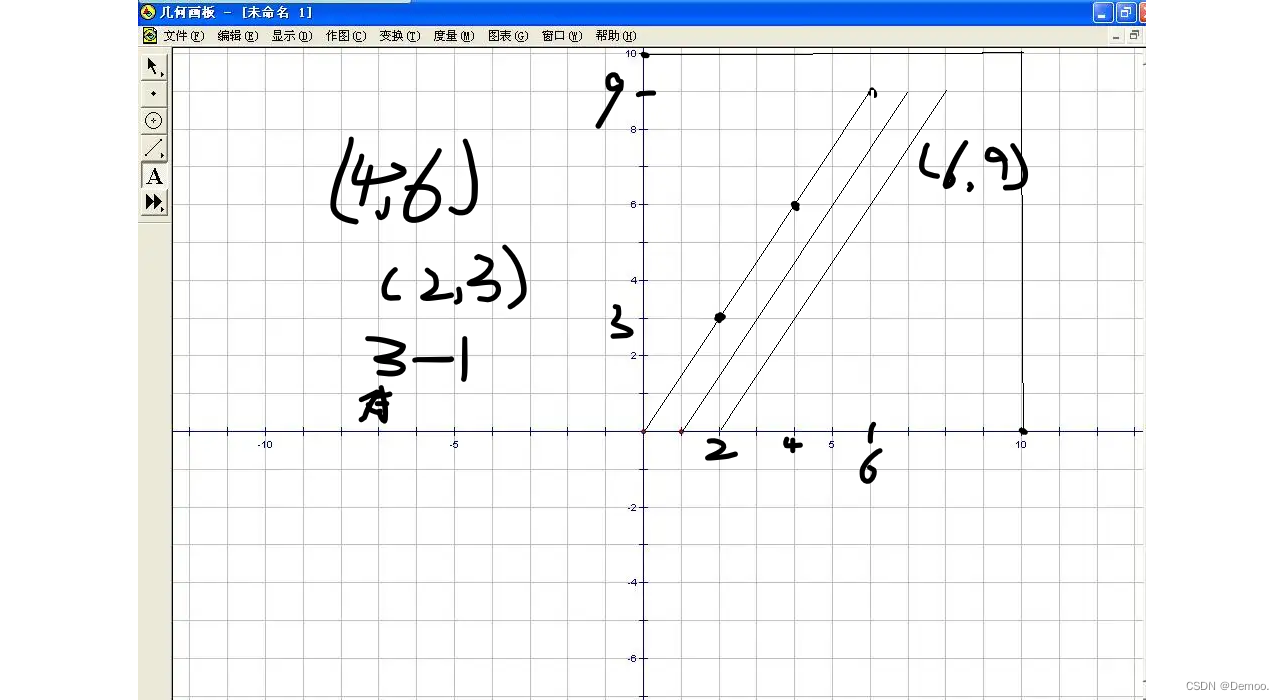
找到的是(2.3)(4.6)(6.9),就是gcd(j,i)
但是我们只要中间的,所以再减去1.
我们只是列举了从0.0开始的斜率,他还可以向右平移,得到的个数就是(n-j+1)个
我们也可以上下平移,得到的个数就是(m-i+1)个
然后这几种情况相乘就是总的个数,也就是最后一个柿子。
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
ll gcd(ll a,ll b)
{
if(a%b==0)
return b;
else return (gcd(b,a%b));
}
ll c(ll m,ll n){
if(m<n)return 0;
if(m==n)return 1;
ll b;
ll a;
if(n>m-n){
b=m-n;
a=n;
}else {
b=n;
a=m-n;
}
ll num1=1,num2=1;
for(int i=m;i>=a+1;i--){
num1*=i;
}
for(int i=1;i<=b;i++){
num2*=i;
}
return num1/num2;
}
int main(){
ll n,m;
cin>>n>>m;
if(n==1&&m==1){
cout<<4;
return 0;
}
ll con=(n+1)*(m+1);
con=c(con,3);
con-=(m+1)*c(n+1,3);
con-=(n+1)*c(m+1,3);
// cout<<"con="<<con<<endl;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
ll num1=(m-j+1)*(n-i+1)*(gcd(i,j)-1);
// cout<<"gcd="<<(gcd(i,j)-1)<<endl;
// cout<<"num1="<<num1<<endl;
con-=(num1*2);
}
}
cout<<con;
return 0;
}
GAME (HDU)(博弈论)
Alice and Bob are playing a game. They take turns and Alice moves first. There is a set of positive integers. In one's turn, he or she can choose a number (suppose xx) in the set, and choose a positive integer kk (kk does not need to be in the set), and replace xx with x-(10^k-1)x−(10k−1). For example, you can make a number xx in the set become x-9x−9 or x-99x−99 or x-999x−999 or x-999\cdotsx−999⋯. After that the set must still be a set of positive integers. That is to say:
* The number must still be positive: x-(10^k-1) > 0x−(10k−1)>0.
* A set can not have duplicate elements: x-(10^k-1)x−(10k−1) can not be equal to any other numbers in the set.
They take turns and Alice moves first. The one who can't move loses the game. Now the question is that who will win the game if they play optimally.
题意:a和b在玩游戏,给你一组正整数,每次可以减9,99,999...,但是要满足两个条件:1.减完之后必须是正整数,2.没有重复的元素
a先移动,不能动的人输,每个人最优,求谁赢
思路:-99,999等等都是9的倍数,最小减的数是9,那么我们就算最多能减多少次9,而且应该先对原数组排序之后再算每个数最多能减多少个9是最优解,
那么我们就先对数组排序再对原数组求最多能减几次9
还有一个问题是不能有重复的数,那我们先算能减的最多的数,然后我们再减去重复的操作数
那么我们对每个数来说,%9余数是0的我们最终的数应该是9 18 27...也就是1*9 2*9 3*9,那么多算的不数就是1 2 3...假设个数为n那么重复的操作数就是n*(n+1)/2
%9!=0的时候:假如余数是op,那我们就变到op+9*0 ,op+9*1,op+9*2...,那么操作数就是 0 1 2 ...,假设有n个余数是op的数,那么重复的操作次数就是n*(n-1)/2
然后用总操作数减去重复的操作数就是最后的操作数了,是单数的话A赢,双数的话是B赢
/*
.----------------. .----------------. .----------------. .----------------.
| .--------------. || .--------------. || .--------------. || .--------------. |
| | ________ | || | _________ | || | ____ ____ | || | ____ | |
| | |_ ___ `. | || | |_ ___ | | || ||_ \ / _|| || | .' `. | |
| | | | `. \ | || | | |_ \_| | || | | \/ | | || | / .--. \ | |
| | | | | | | || | | _| _ | || | | |\ /| | | || | | | | | | |
| | _| |___.' / | || | _| |___/ | | || | _| |_\/_| |_ | || | \ `--' / | |
| | |________.' | || | |_________| | || ||_____||_____|| || | `.____.' | |
| | | || | | || | | || | | |
| '--------------' || '--------------' || '--------------' || '--------------' |
'----------------' '----------------' '----------------' '----------------'
*/
#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
#include<set>
#include<map>
#include<queue>
#include<deque>
#include<cmath>
#include<stack>
#define int long long
#define lowbit(x) x&(-x)
#define PI 3.1415926535
#define endl "\n"
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
int gcd(int a,int b){
return b>0 ? gcd(b,a%b):a;
}
/*
int dx[8]={-2,-2,-1,1,2,2,-1,1};
int dy[8]={-1,1,2,2,1,-1,-2,-2};
int dx[4]={0,-1,0,1};
int dy[4]={-1,0,1,0};
int dx[8]={-1,1,0,0,-1,-1,1,1};
int dy[8]={0,0,-1,1,-1,1,-1,1};
*/
//int e[N],ne[N],h[N],idx,w[N];
/*void add(int a,int b,int c){
e[idx]=b;
w[idx]=c;
ne[idx]=h[a];
h[a]=idx++;
}
*/
const int N=2e5+10;
int n;
int a[N],b[N],c[N],book[N];
signed main(){
ios::sync_with_stdio(false);
cin.tie() ,cout.tie() ;
while(cin>>n){
for(int i=0;i<=9;i++){
book[i]=0;
}
for(int i=1;i<=n;i++){
cin>>a[i];
}
sort(a+1,a+1+n);
int ans=0;
for(int i=1;i<=n;i++){
b[i]=a[i]/9;
c[i]=a[i]%9;
ans+=b[i];
book[c[i]]++;
}
for(int i=0;i<=8;i++){
int k;
if(i==0){
k=book[i]*(book[i]+1)/2;
}else k=book[i]*(book[i]-1)/2;
ans-=k;
}
if(ans&1){
cout<<"A"<<endl;
}else cout<<"B"<<endl;
}
}
CF340C Tourist Problem
题目描述
Iahub is a big fan of tourists. He wants to become a tourist himself, so he planned a trip. There are nn destinations on a straight road that Iahub wants to visit. Iahub starts the excursion from kilometer 0. The nn destinations are described by a non-negative integers sequence a_{1}a1 , a_{2}a2 , ..., a_{n}an . The number a_{k}ak represents that the kk th destination is at distance a_{k}ak kilometers from the starting point. No two destinations are located in the same place.
Iahub wants to visit each destination only once. Note that, crossing through a destination is not considered visiting, unless Iahub explicitly wants to visit it at that point. Also, after Iahub visits his last destination, he doesn't come back to kilometer 0, as he stops his trip at the last destination.
The distance between destination located at kilometer xx and next destination, located at kilometer yy , is |x-y|∣x−y∣ kilometers. We call a "route" an order of visiting the destinations. Iahub can visit destinations in any order he wants, as long as he visits all nn destinations and he doesn't visit a destination more than once.
Iahub starts writing out on a paper all possible routes and for each of them, he notes the total distance he would walk. He's interested in the average number of kilometers he would walk by choosing a route. As he got bored of writing out all the routes, he asks you to help him.
输入格式
The first line contains integer nn ( 2<=n<=10^{5}2<=n<=105 ). Next line contains nn distinct integers a_{1}a1 , a_{2}a2 , ..., a_{n}an ( 1<=a_{i}<=10^{7}1<=ai<=107 ).
输出格式
Output two integers — the numerator and denominator of a fraction which is equal to the wanted average number. The fraction must be irreducible.
题意翻译
给定一条直线上n个点的坐标a_1,a_2,...a_na1,a2,...an,一条路线从原点开始,经过aa的一个排列并在最后一个点结束(也就是说不返回原点)。一条路径的长度定义为排列中相邻两点x,yx,y的距离|x-y|∣x−y∣(包括原点),求所有路线的平均长度,要求化为最简分数。
输入输出样例
输入 #1复制
3 2 3 5
输出 #1复制
22 3
题意:有n个地点。
每个地点离原点的距离是a[i]。
任意两个地点i,j的距离是|a[i]-a[j]|。
求所有走过每个地点且只经过一次的路线的平均值(最简分母和分子)。
思路:经过每个点的所有路线的条数是n的全排列(n!)。
因为我们在算的时候是两个地点挨在一起的绝对值,所以不妨就令大的值减去小的值。
那这一步我们就可以从大到小将a数组排序,然后我们再观察所有路线。
拿例题举例:
2 3 5
全排列之后的所有可能方法是
2 3 5:(2-0)+(3-2)+(5-3)
2 5 3:(2-0)+(5-2)+(5-3)
3 2 5:(3-0)+(3-2)+(5-2)
3 5 2:(3-0)+(5-3)+(5-2)
5 2 3:(5-0)+(5-2)+(3-2)
5 3 2:(5-0)+(5-3)+(3-2)
然后我们可以观察出来与3相关的运算:
(3-2)(3-2) (3-2)(3-2)(5-3)(5-3)(5-3)(5-3)(3-0)(3-0)
(3-0)的情况就是用3开头的时候有几种情况,那么就是除了3剩下的数全排列即2!
那么3就加了2!次,即(n-1)!次。
再分析3和数组中其他数的相减情况:
可以观察出他可以和数组中每个数都能相邻
下标从1开始。
且和每一个数相邻的情况一共有A22*A22种(先挑一个数和他捆起来,然后内部全排列是A22个,之后把捆起来的看成一个整体,再让这个整体来全排列),用通式就是2*(n-1)!
然后我们再看他和每个数相邻是怎么计算的
我们把数组从大到小排序:5 3 2
他可以是和5挨着也可以是和2挨着,当和5挨着的时候就是5-3,当和2挨着的时候就是3-2
那么总结的来说就是他前面的数减去他,他后面的数加上他
所以他自己被加了(n-i)次,被减了(i-1)次。
那么我们就可以得出a[i]在总的运算来说,参与运算的柿子是:
a[i]*(n-1)!+2*(n-1)!*(a[i]*(n-i)-a[i]*(i-1))
那么总数就是从1~n的所有a[i]*(n-1)!+2*(n-1)!*(a[i]*(n-1)-a[i]*(i-1))相加
化简一下:(n-1)!*(a[i]+2*(a[i]*(n-i) )
然后我们要求总数除以路线条数
路线条数是n!
我们先化简一下就是(a[i]+2*(a[i]*(n-i))/n
然后我们就只需要算出i从1~n,(a[i]+2*(a[i]*(n-i))的值
然后输出他们各自除以他们的最大公约数了。
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
const ll N=1e5+7;
ll a[N];
ll n;
ll gcd(ll a,ll b){
if(a<b)swap(a,b);
if(b!=0){
return gcd(b,a%b);
}return a;
}
int main(){
ios::sync_with_stdio(false);
cin.tie() ,cout.tie() ;
cin>>n;
ll sum=0;
for(int i=1;i<=n;i++){
cin>>a[i];
sum+=a[i];
}
ll ans=0;
sort(a+1,a+n+1,greater<int>());
for(int i=1;i<=n;i++){
ans+=(a[i]*(n-2*i+1));
}
ans*=2;
ans+=sum;
ll m=gcd(ans,n);
cout<<ans/m<<" "<<n/m;
return 0;
}
