前缀和，差分

设原数组为a[i]

前缀和

一维前缀和

前缀和数组：s[i]=a[1]+a[2]+a[3]+...+a[i]

如何求：i:1~n,s[i]=s[i-1]+s[i]

作用：快速的求出原数组中一段数组的和

比如：求a数组中第l个数到第r个数的和

s[r]=a[1]+a[2]+...+a[l-1]+a[l]+a[l+1]+...+a[r]

我们要求a[l]+a[l+1]+...+a[r]的和，那么我们需要将s[r]前面的a[1]+a[2]+...+a[l-1]减去，那么这些数相加刚好是s[l-1]

所以求a[l~r]的和，就是s[r]-s[l-1]

例题：给出一个n个数的数组，q组询问，每次询问给出两个数l和r，求数组中第l个数到第r个数的和

#include<iostream>
#include<algorithm>
using namespace std;
int n,q,l,r;
const int N=1e5+10;
int a[N],s[N];
int main(){
    cin>>n>>q;
    for(int i=1;i<=n;i++)cin>>a[i];
    for(int i=1;i<=n;i++)s[i]=s[i-1]+a[i];
    while(q--){
        cin>>l>>r;
        cout<<s[r]-s[l-1]<<endl;
    }
    return 0;
}

二维前缀和

给出一个n*m的二维数组，求以a[x1][y1]为左上角，a[x2][y2]为右下角的矩形区域内的数的和

设s[i][j]表示以a[1][1]为左上角，a[i][j]为右下角的矩形部分内数的和

如何算s[i][j]：

如下图：s[i][j]框起的绿色区域表示以a[i][j]为右下角，a[1][1]为左上角的矩形区域的数的和，s[i][j-1]框起的红色区域和s[i-1][j]框起的紫色区域以及s[i-1][j-1]框起的蓝色区域皆是以a[1][1]为左上角，其坐标为右下角的矩形区域的数的和

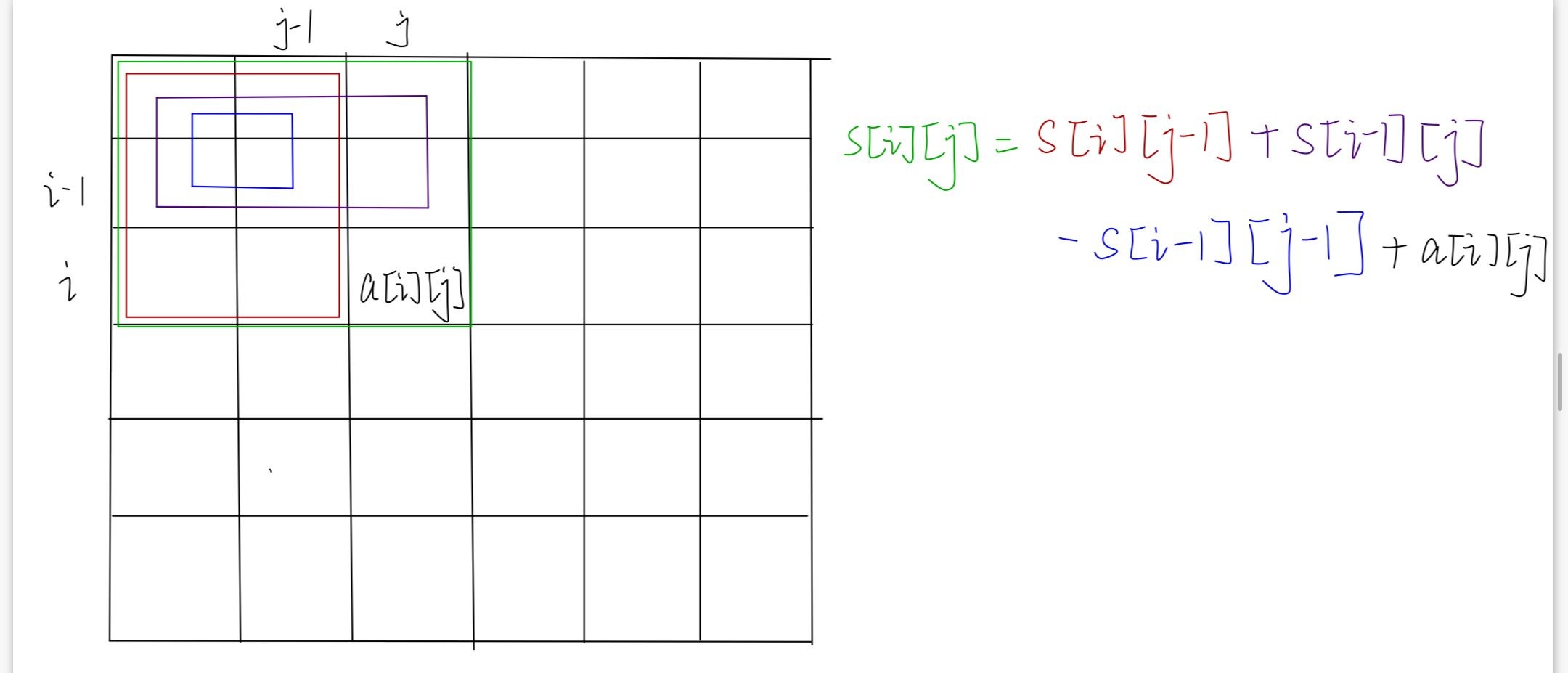
那么绿色区域=红色区域+紫色区域-蓝色区域+a[i][j]，即s[i][j]=s[i][j-1]+s[i-1][j]-s[i-1][j-1]+a[i][j],s[i][j]得以算出

如何算以a[x1][y1]为左上角，a[x2][y2]为右下角的矩形区域内的数的和：

如下图：s框起的绿色区域表示我们需要找的区域，s[x2][y2]表示框起的红色区域，s[x2][y1-1]表示框起的紫色区域，s[x1-1][y2]表示框起的蓝色区域，s[x1-1][y1-1]表示框起的黄色区域

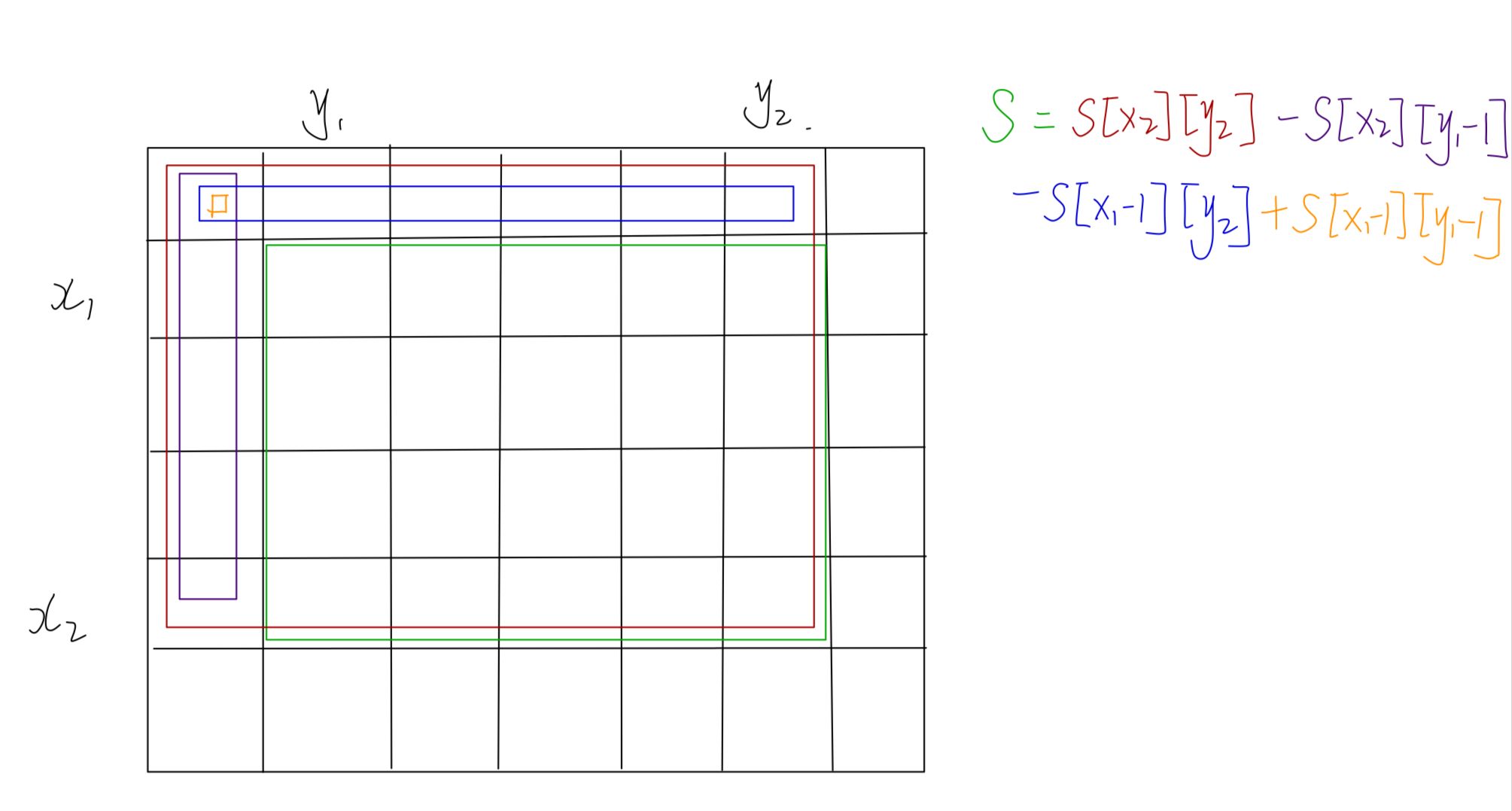
绿色区域=红色区域-紫色区域-绿色区域+黄色区域，即s=s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1]

例题：给出一个n*m的二维数组，有q个询问，每个询问给出x1,y1,x2,y2，求以a[x1][y1]为左上角，a[x2][y2]为右下角的矩形区域内的数的和

#include<iostream>
#include<algorithm>
using namespace std;

int n,m,q;
const int N=1005;
int a[N][N],s[N][N];

int main(){
    cin>>n>>m>>q;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            cin>>a[i][j];
            s[i][j]=s[i][j-1]+s[i-1][j]-s[i-1][j-1]+a[i][j];
        }
    }
    while(q--){
        int x1,y1,x2,y2;
        cin>>x1>>y1>>x2>>y2;
        cout<<s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1]<<endl;
    }
    return 0;
}

差分

一维差分

a[i]的差分数组：b[i]=a[i]-a[i-1]

那么可以发现：b[1]+b[2]+b[3]+...b[i]=a[1]-a[0]+a[2]-a[1]+a[3]-a[2]+...+a[i]-a[i-1]=a[i]

所以b[i]是a[i]的差分数组，a[i]是b[i]的前缀和数组，那么如果已知b数组求a数组，只需要对b数组求前缀和就可以了

作用：可以在O（1）的时间对a[l~r]的所有数全部加减c

那么原数组a[i]为b[i]的前缀和，如图

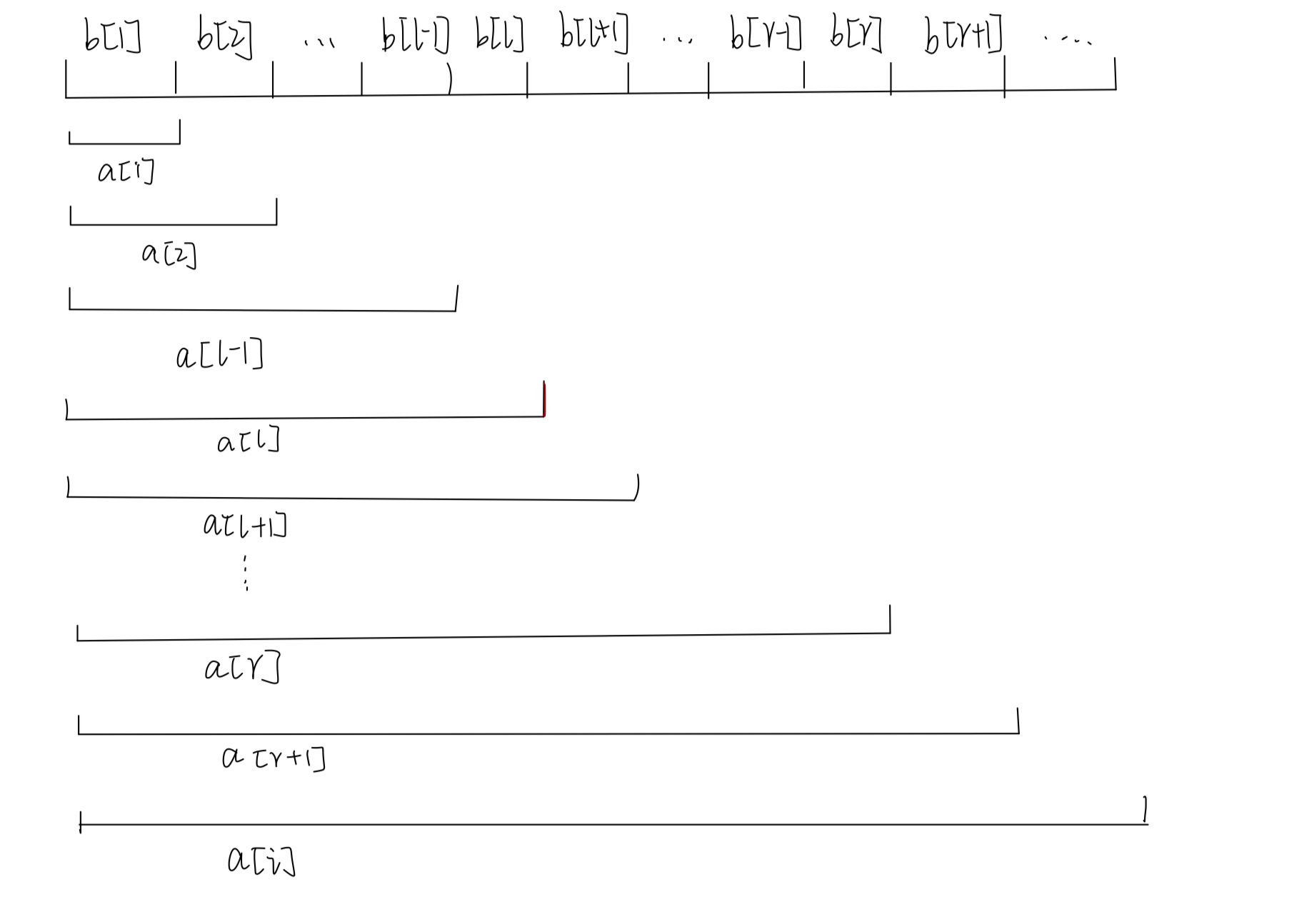
那么我们执行一个操作：b[l]+c,通过下图我们可以观察到，对变化后的b数组进行前缀和操作之后，a[l]往后的所有数都在原来的基础上+c了

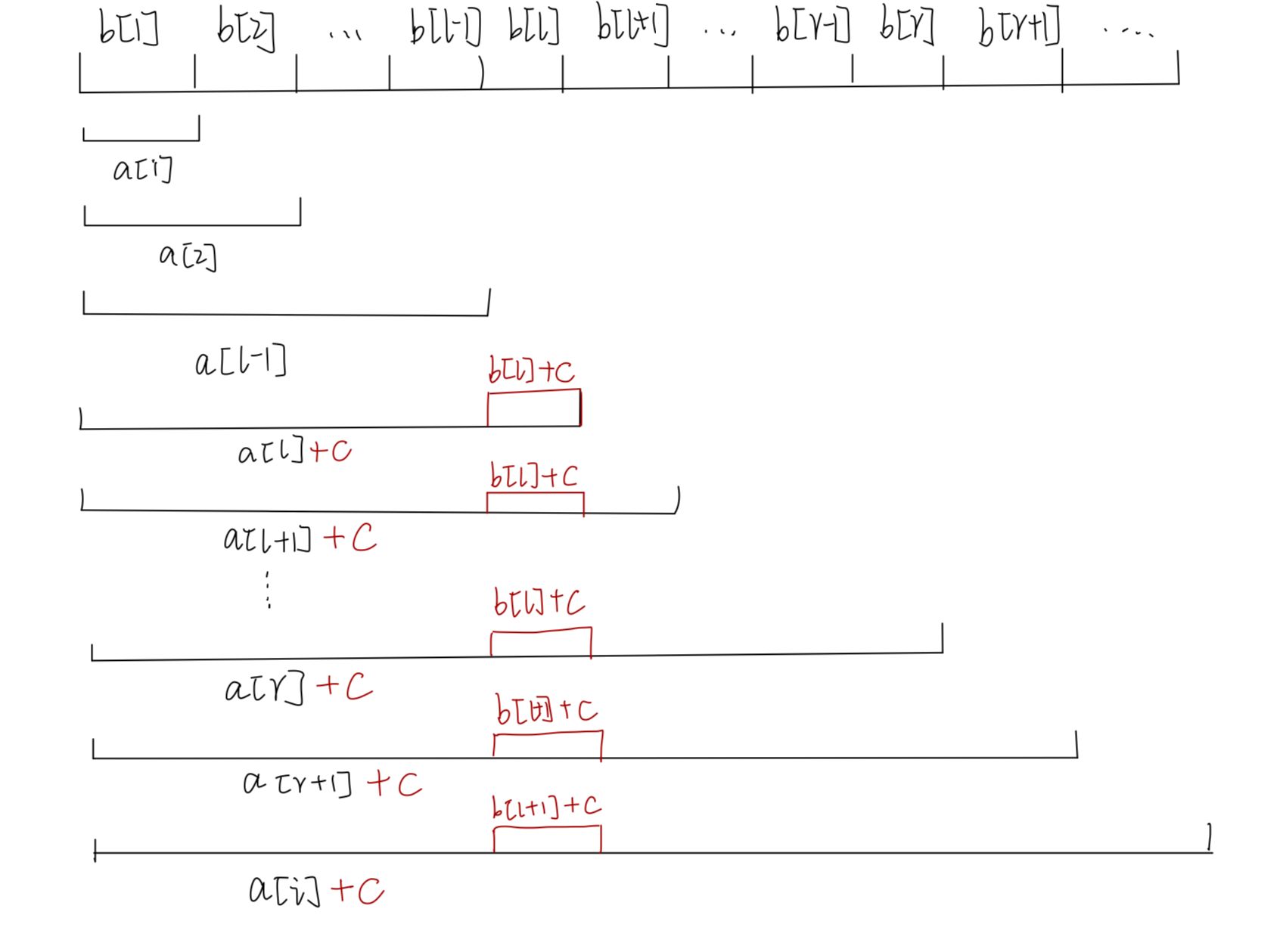
但是我们只需要将a[l_{r]内的所有数都加上c，那么由于对b[i]+c，其前缀和数组a[i}n]+c,那么我们再将b[r+1]-c，那么其前缀和数组a[r+1_{n]就又减去了c，那么a[r+1}n]+c-c=a[r+1~n]，所以后面的数+c和-c抵消，就只对[l,r]这一区间的数都+c

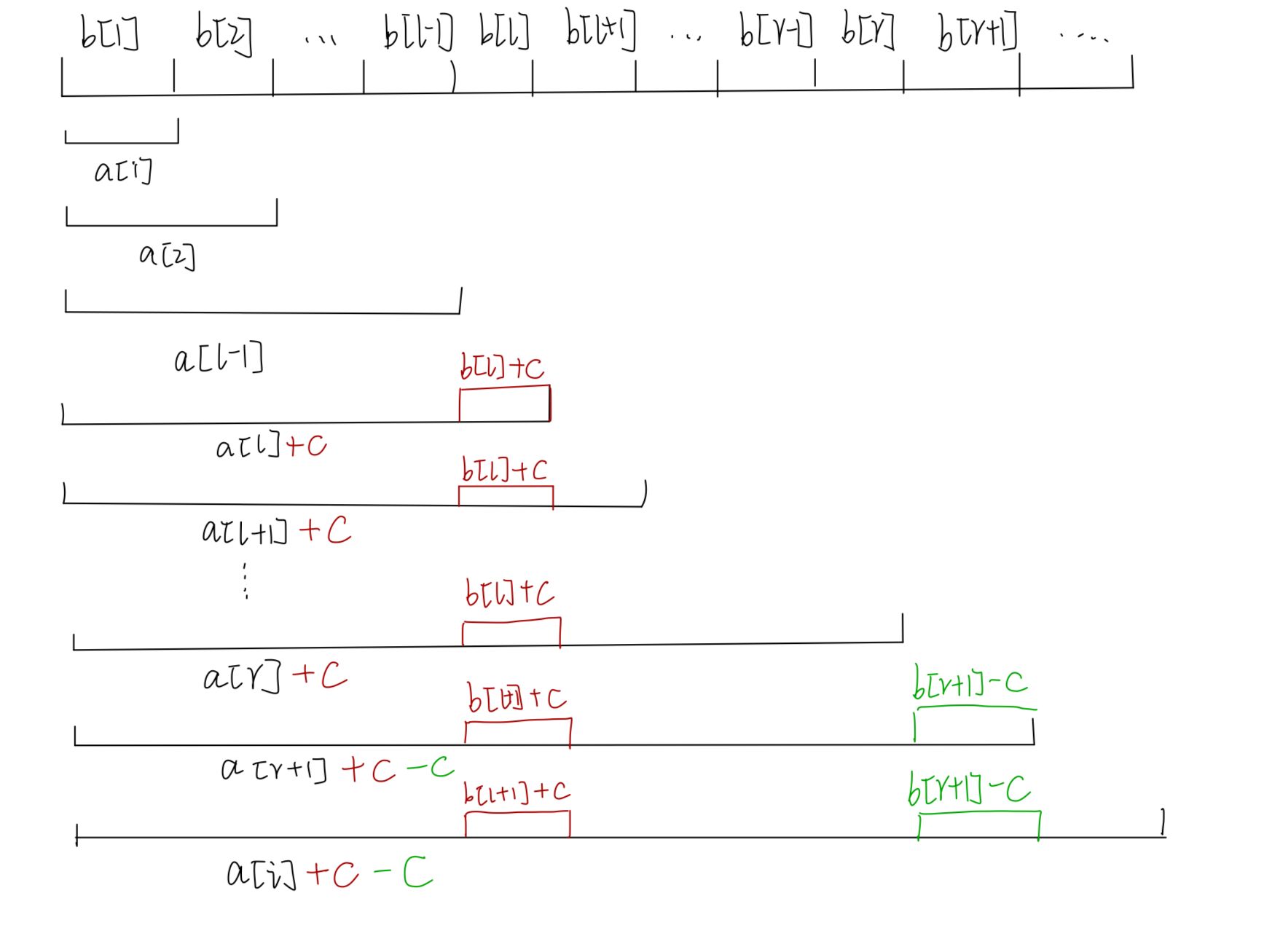
那么a数组的[l,r]内所有数都+c，只需要对b数组进行两个操作：b[l]+1,b[r+1]-c，然后对b数组求前缀和就可以了

例题：一个数组有n个数，q个操作，每个操作给出三个数l，r，c，表示在a[l~r]的每个数+c，求q个操作之后的数组

#include<iostream>
#include<algorithm>
using namespace std;
const int N=1e5+10;
int n,q;
int a[N],b[N];

int main(){
    cin>>n>>q;
    for(int i=1;i<=n;i++){
        cin>>a[i];
        b[i]=a[i]-a[i-1];
    }
    while(q--){
        int l,r,c;
        cin>>l>>r>>c;
        b[l]+=c;
        if(r+1<=n)b[r+1]-=c;
    }
    for(int i=1;i<=n;i++){
        a[i]=a[i-1]+b[i];
        cout<<a[i]<<" ";
    }
    return 0;
}

二维差分

作用：对于一个二维矩阵，将以a[x1][y1]为左上角，a[x2][y2]为右下角的矩形区域内的所有数都+c

构造b[i][j]使得a[i][j]是b[i][j]的前缀和数组，即a[i][j]是以b[1][1]为左上角，b[i][j]为右下角，是区域内所有b的和

用a[i][j]构造b[i][j]：a[i][j]为红色区域，a[i-1][j]为绿色区域，a[i][j-1]为蓝色区域，a[i-1][j-1]为玫红区域，那么b[i][j]=红色区域-绿色区域-蓝色区域+玫红区域，即b[i][j]=a[i][j]-a[i-1][j]-a[i][j-1]+a[i-1][j-1]

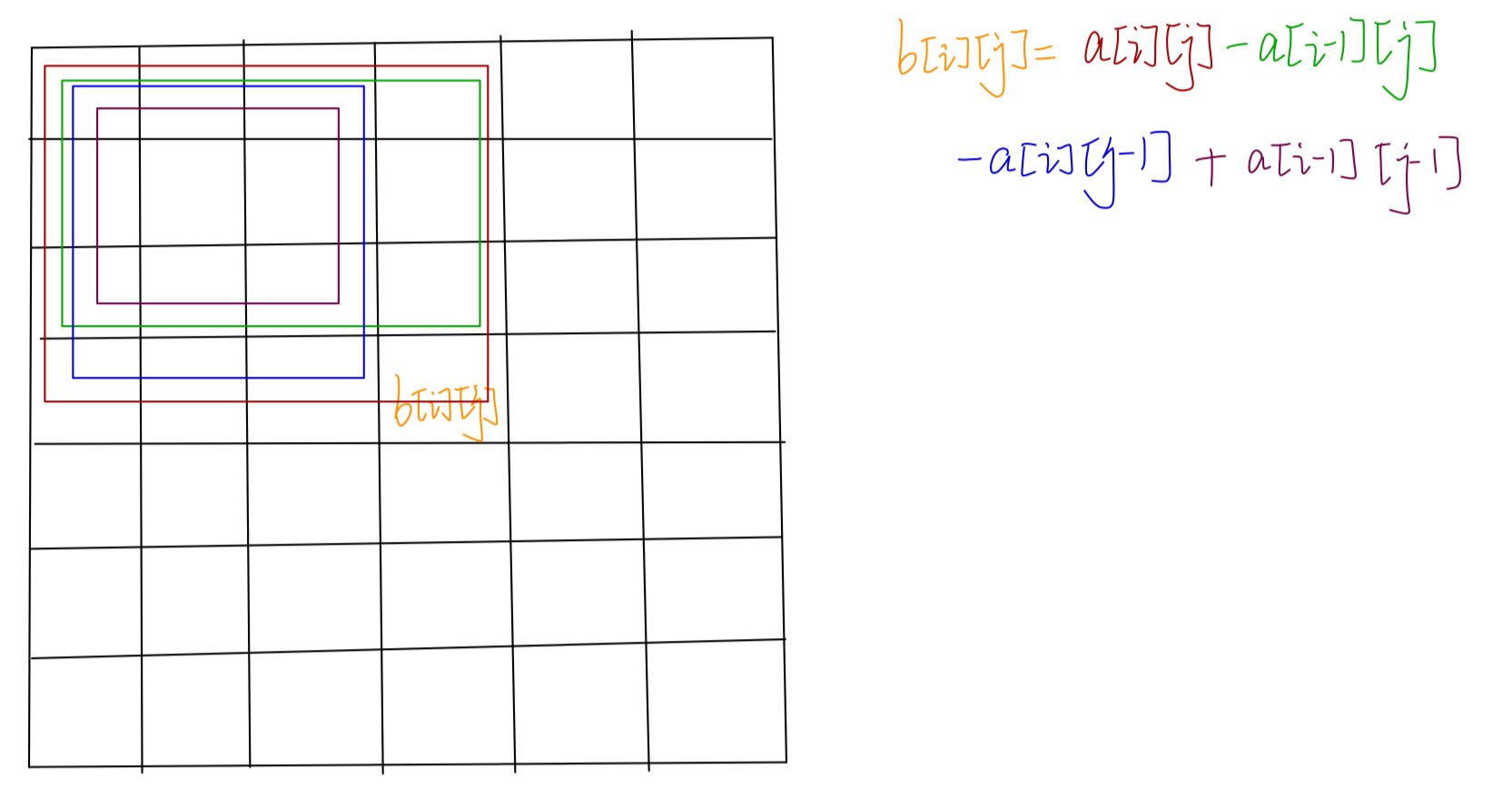
把以a[x1][y1]为左上角，a[x2][y2]为右下角的区域中所有数都+c。

如图，下图显示的是a[i][j]数组，当b[x1][y1]+c之后，前缀和数组a[x1][y1]的右下所有的a都+c，如图的红色区域

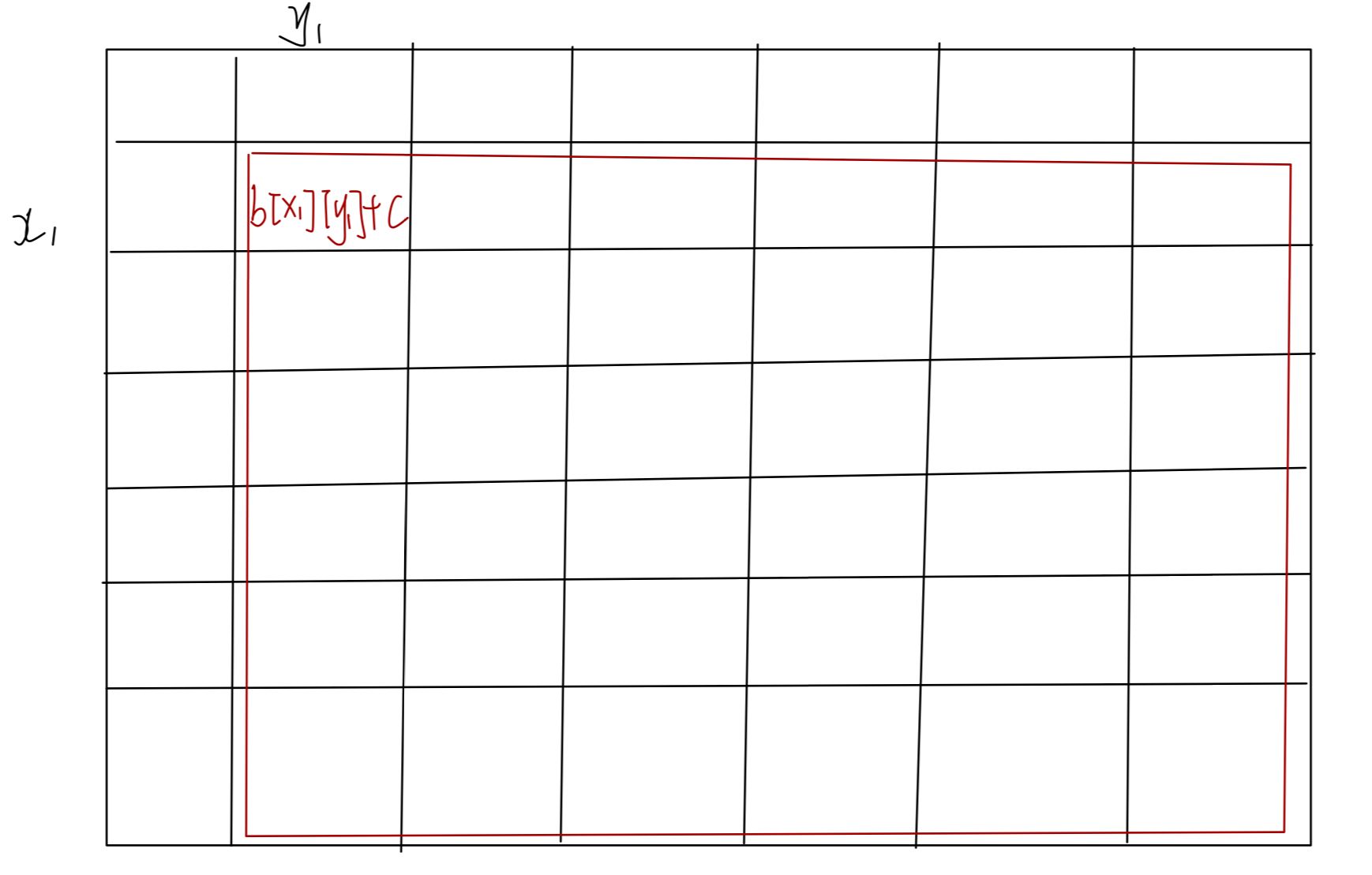
但是我们只需要以a[x1][y1]为左上角，a[x2][y2]为右下角的矩形区域内的所有a数组+c，那么我们就需要减去多余部分

那么b[x2+1][y1]-c，就是绿色部分-c，b[x1][y2+1]-c,就是蓝色部分-c，b[x2+1][y2+1]+c，就是橙色部分+c，最后+c-c相抵消，就只有需要的区域+c了

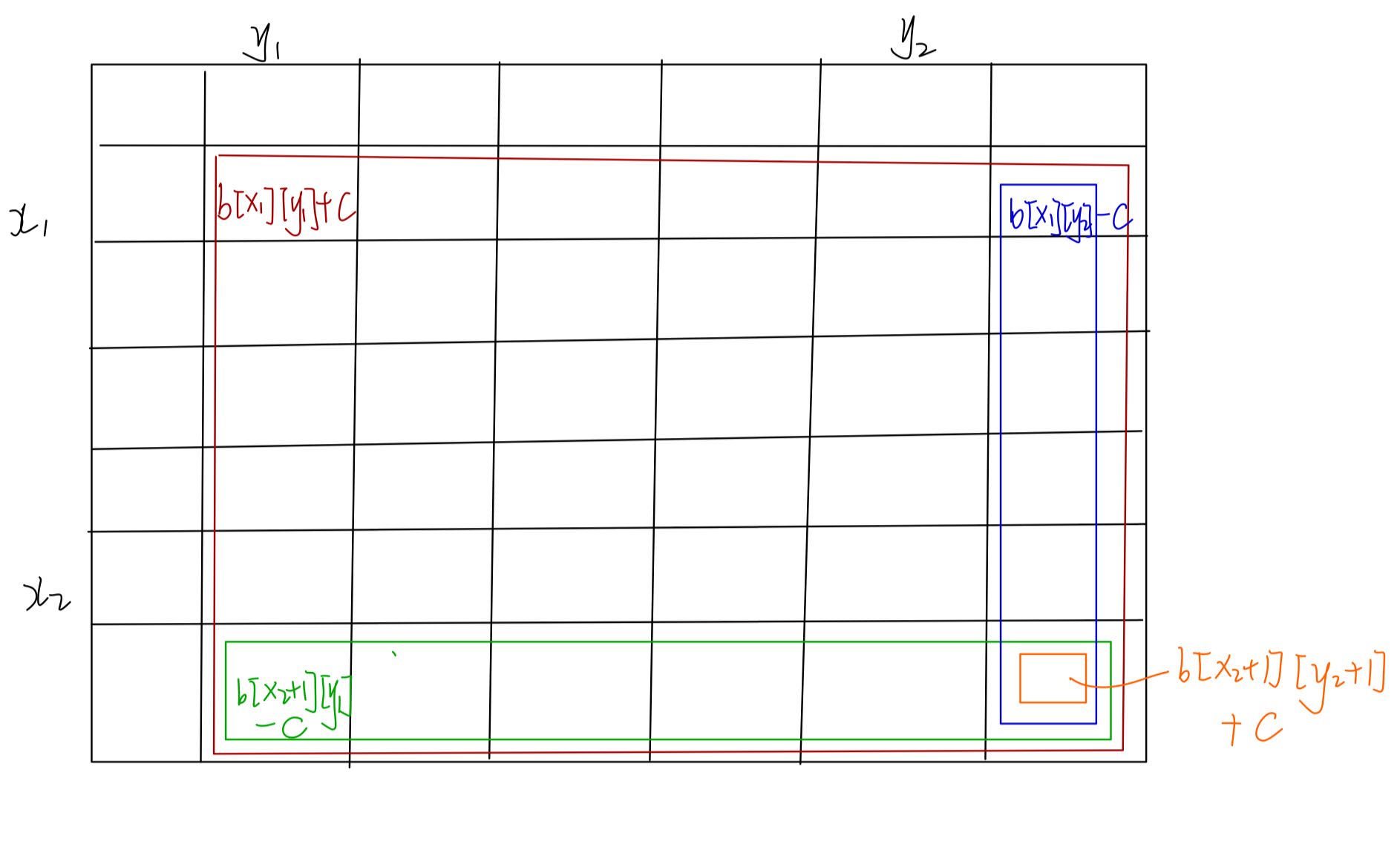
所以需要的操作就是：b[x1][y1]+c，b[x2+1][y2]-c，b[x1][y2+1]-c，b[x2+1][y2+1]+c

最后要求a[i][j]矩阵的时候，我们只需要将初始化时求b[i][j]的等式：b[i][j]=a[i][j]-a[i-1][j]-a[i][j-1]+a[i-1][j-1]
等价变化为：a[i][j]=b[i][j]+a[i-1][j]+a[i][j-1]-a[i-1][j-1]

a数组即可算出

例题：一个n*m的二维数组，右q个操作，每个操作给出x1,y1,x2,y2,c，表示将以a[x1][y1]为左上角，a[x2][y2]为右下角的区域+c。求q个操作之后的数组

#include<iostream>
#include<algorithm>
using namespace std;
int n,m,q;
const int N=1005;
int a[N][N],b[N][N];
int c,x1,y1,x2,y2;

int main(){
    cin>>n>>m>>q;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            cin>>a[i][j];
            b[i][j]=a[i][j]-a[i-1][j]-a[i][j-1]+a[i-1][j-1];
        }
    }
    while(q--){
        cin>>x1>>y1>>x2>>y2>>c;
        b[x1][y1]+=c;
        if(x2+1<=n)b[x2+1][y1]-=c;
        if(y2+1<=m)b[x1][y2+1]-=c;
        if(x2+1<=n&&y2+1<=m)b[x2+1][y2+1]+=c;
    }

    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            a[i][j]=b[i][j]+a[i-1][j]+a[i][j-1]-a[i-1][j-1];
            cout<<a[i][j]<<" ";
        }
        cout<<endl;
    }
    
    return 0;
}